intg
定積分
呼び出し手順
[v, err] = intg(a, b, f) [v, err] = intg(a, b, f, atol) [v, err] = intg(a, b, f, atol, rtol) [v, err, ierr] = intg(..)
引数
- a, b
- 実数
- f
- 外部 (関数またはリストまたは文字列)
- atol
- 実数. 結果に指定する絶対誤. デフォルト値: 1.d-13.
- rtol
- 実数. 結果に指定する相対誤差. デフォルト値: 1.d-8.
- err
- 結果に関する絶対誤差の推定値.
- ierr
- エラーフラグ番号(エラーが発生しなかった場合は 0).
説明
intg(a,b,f) は,
f(t)dtの
a から bまでの
定積分を計算します.
関数 f(t) は連続である必要があります.
この計算は以下の精度を満たすことが期待されます:
abs(I-v)<= max(atol, rtol*abs(I)) ただし
I はこの積分の真値を意味します.
f は以下のような外部ルーチンです :
f が関数の場合,
y = f(t) のように定義されている必要があります.
f がリストの場合,
このリストは以下のようである必要があります:
list(f,x1,x2,...) ただし f
は呼び出し手順が f(t,x1,x2,...) の関数です.
f が文字列の場合,
以下の規定の呼出し手順を有する
Fortran関数またはCプロシージャの名前を指しています:
Fortran の場合, 呼出し手順は
double precision function f(x) とします.
ただし, x も倍精度実数となります.
Cの場合, 呼出し手順は double
f(double *x)
とします.
使用される関数 : 関連するルーチンは SCI/modules/differential_equations/src/fortran ディレクトリにあります : quadpackのdqags.f および dqagse.f
既知の制限
他の積分ルーチンと同様に intg は
スパイク欠損の制約を受けます.
スパイクを有するフラットな関数は, スパイクが十分にスティフな場合には完全にフラットな関数に見えます.
これは回避できず,積分処理の動作をよく知ることが必要です.
つまり, intgは 21点 Gauss-Kronrod法を
使用します.
このため, 2つの連続する積分点の間にスパイクがある場合,
検出されず, この関数はスムーズであるとみなされます.
しかし, 関数が非常にスムースな場合には警告メッセージが発行されます. この際,ユーザは積分区間を減らすよう提案されており, スパイクを見失っていないかを検討する必要があります.
以下のグラフがこの現象を図示しています:
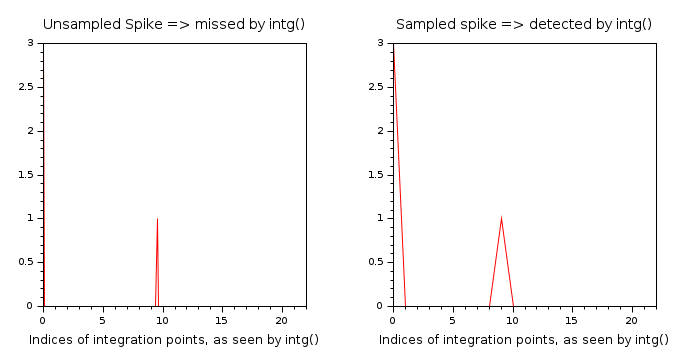
On the left image, the spike lays between the 9th and 10th integration points,
and is not detected. intg considers the function flat.
On the right, the spike is large enough to be covered by the integration points.
 | ソルバがエラーを発生した場合でも, ユーザが計算された回を表示しようとすると,
3番目の出力引数 ierrを追加する必要があり,
これによりエラーを警告に変換します. これは主に丸め誤差の場合に使用されます. |
例
//Scilabで記述された外部関数 function y=f(x), y = x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)), endfunction exact = -2.5432596188; I = intg(0, 2*%pi, f) abs(exact - I) //1つの引数を有するScilabで記述された関数 function y=f1(x, w), y = x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)), endfunction I = intg(0, 2*%pi, list(f1,30)) abs(exact-I) // Fortranで記述された外部関数 (Fortranコンパイラが必要) // Fortranコードの記述 cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F,'ffun.f') // Fortranコードをコンパイル l = ilib_for_link('ffun', 'ffun.f', [], 'f'); // インクリメンタルリンクの実行 link(l, 'ffun', 'f') // 関数の積分 I = intg(0, 2*%pi, 'ffun') abs(exact - I) // Cで記述された外部関数 (Cコンパイラが必要) // Cコードの記述 C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C, 'cfun.c') // Cコードをコンパイル l = ilib_for_link('cfun', 'cfun.c', [], 'c'); // インクリメンタルリンクの実行 link(l, 'cfun', 'c') // 関数の積分 I = intg(0, 2*%pi, 'cfun') abs(exact - I)
参照
履歴
| バージョン | 記述 |
| 6.0.2 | The default value atol of the absolute tolerance is increased from 10-14 to 10-13. |
| Report an issue | ||
| << integrate | 微分方程式 | intl >> |