intg
intégration numérique adaptative
Séquence d'appel
[v, err] = intg(a, b, f) [v, err] = intg(a, b, f, atol) [v, err] = intg(a, b, f, atol, rtol) [v, err, ierr] = intg(..)
Paramètres
- a, b
- nombres réels finis : bornes de l'intégrale.
- f
- fonction à intégrer, spécifiée soit par son nom litéral (ex: "sind"), soit par son identifiant (ex : sind), soit par une liste (si la fonction attend en outre des paramètres).
- atol
- nombre réel positif : erreur absolue maximale tolérée sur le résultat (1.d-13 par défaut).
- rtol
- nombre réel positif : erreur relative maximale tolérée sur le résultat (1.d-8 par défaut).
- err
- estimation de l'erreur absolue sur le résultat.
- ierr
- numéro d'erreur (= 0 si absence d'erreur).
Description
intg(a,b,f) approche l'intégrale de
a à b de f(t)dt.
La fonction f doit être continue.
L'évaluation satisfait si possible abs(I-v)<=
max(atol,er*abs(I))
où I représente la valeur exacte de
l'intégrale.
f est une fonction externe :
Si f est une fonction Scilab elle doit avoir la
liste d'appel : y = f(t)
Si f est une liste, cette liste doit avoir la
structure suivante : list(f,x1,x2,...) où
f est une fonction Scilab avec la liste d'appel :
f(t,x1,x2,...).
Si f est une chaîne de caractères, ce paramètre
désigne le nom d'un fonction Fortran ou d'une procédure C ayant une liste
d'appel fixée:
Dans le cas Fortran la liste d'appel doit être: double
precision function f(x)
où x est aussi un
nombre double precision.
Dans le cas d'une fonction en C, la liste d'appel doit être:
double f(double *x).
Fonctions Utilisées : les programmes correspondants (dqags.f et dqagse.f de quadpack) se trouvent dans le répertoire SCI/modules/differential_equations/src/fortran/.
Limitation connue
Comme tous les intégrateurs, intg est susceptible de manquer des pics.
Une fonction plate contenant un pic sera considérée totalement plate si le pic est suffisamment raide.
Cela ne peut pas être évité. On comprend facilement pourquoi dès que l'on comprend
comment l'intégrateur opère.
En effet, intg utilise la méthode des 21 points de Gauss-Kronrod.
Ainsi, s'il y a un pic entre deux points d'intégration consécutifs,
il ne sera pas détecté. La fonction sera localement considérée comme lisse.
Cependant, un warning s'affichera si la fonction est considérée très lisse, qui suggèrera à l'utilisateur de réduire l'intervalle d'intégration, s'il pense que des pics ont été manqués.
Les graphes suivants illustrent ce phénomène :
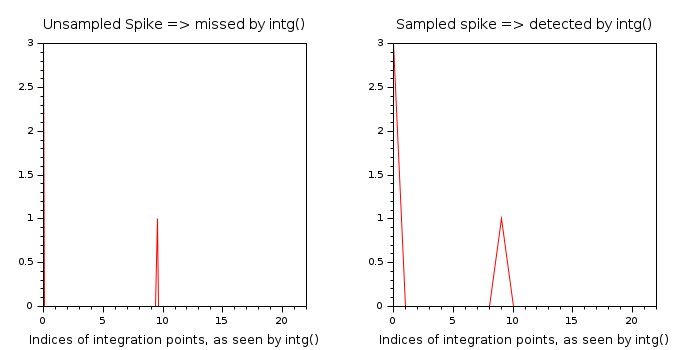
Sur le graphe de gauche, le pic réside entre les points d'intégration n° 9 et 10.
Il n'est pas détecté. intg considère la fonction comme plate.
À droite, le pic est suffisamment large pour être échantillonné par intg().
 | Si l'utilisateur veut afficher la solution même si le solveur a rencontré une erreur,
il doit ajouter le troisième argument de sortie ierr, ce qui transformera
les erreurs en warnings. Ceci est surtout utilisé dans les cas d'erreurs d'arrondi. |
Exemples
// External écrit en Scilab function y=f(x), y = x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)), endfunction exact = -2.5432596188; I = intg(0, 2*%pi, f) abs(exact - I) // External écrit en Scilab avec un argument function y=f1(x, w), y = x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)), endfunction I = intg(0, 2*%pi, list(f1,30)) abs(exact - I) // External écrit en Fortran (un compilateur Fortran est nécessaire) // Ecriture du code fortran cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F, 'ffun.f') // compilation du code Fortran l = ilib_for_link('ffun','ffun.f',[],'f'); // link incrémental link(l,'ffun','f') // integration de la fonction I = intg(0, 2*%pi, 'ffun') abs(exact - I) // External écrit en C (un compilateur C est nécessaire) // Ecriture du code C C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C,'cfun.c') // compilation du code C l = ilib_for_link('cfun', 'cfun.c', [], 'c'); // incremental linking link(l, 'cfun', 'c') // integration de la fonction I = intg(0, 2*%pi, 'cfun') abs(exact - I)
Voir aussi
- intc — intégrale dans le plan complexe, selon un chemin rectiligne
- intl — Cauchy integral along a circular arc
- inttrap — intégration approchée de données expérimentales avec la méthode des trapèzes.
- intsplin — intégration approchée de données expérimentales utilisant une interpolation par une spline.
- ode — solveur d'équations différentielles ordinaires
Historique
| Version | Description |
| 6.0.2 | La valeur par défaut atol de l'erreur absolue passe de 10-14 à 10-13. |
| Report an issue | ||
| << integrate | Equations différentielles | intl >> |