csim

Arguments

u

function, list or string (control)

t

real vector specifying times with, t(1) is the initial time (x0=x(t(1))).

sl

syslin list (SIMO linear system) in continuous time.

y

a matrix such that y=[y(t(i)], i=1,..,n

x

a matrix such that x=[x(t(i)], i=1,..,n

tol

a 2 vector [atol rtol] defining absolute and relative tolerances for ode solver (see ode)

Description

simulation of the controlled linear system sl. sl is assumed to be a continuous-time system represented by a syslin list.

u is the control and x0 the initial state.

y is the output and x the state.

The control can be:

1. a function : [inputs]=u(t)

2. a list : list(ut,parameter1,....,parametern) such that: inputs=ut(t,parameter1,....,parametern) (ut is a function)

3. the string "impuls" for impulse response calculation (here sl must have a single input and x0=0). For systems with direct feedthrough, the infinite pulse at t=0 is ignored.

4. the string "step" for step response calculation (here sl must have a single input and x0=0)

5. a vector giving the values of u corresponding to each t value.

Examples

s=poly(0,'s');
rand('seed',0);
w=ssrand(1,1,3);
w('A')=w('A')-2*eye();
t=0:0.05:5;
//impulse(w) = step (s * w)
plot2d([t',t'],[(csim('step',t,tf2ss(s)*w))',0*t'])

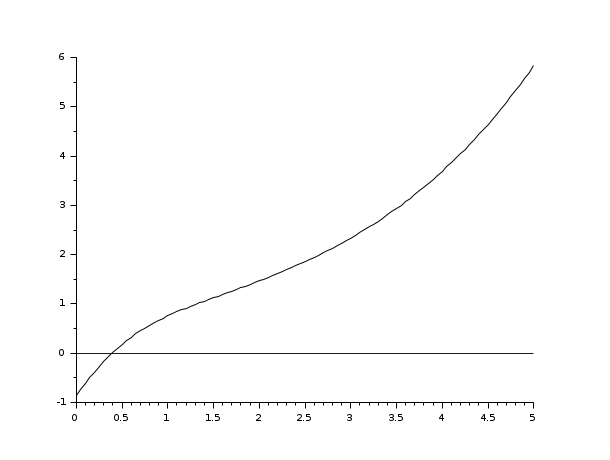
s=poly(0,'s');
rand('seed',0);
w=ssrand(1,1,3);
w('A')=w('A')-2*eye();
t=0:0.05:5;
plot2d([t',t'],[(csim('impulse',t,w))',0*t'])

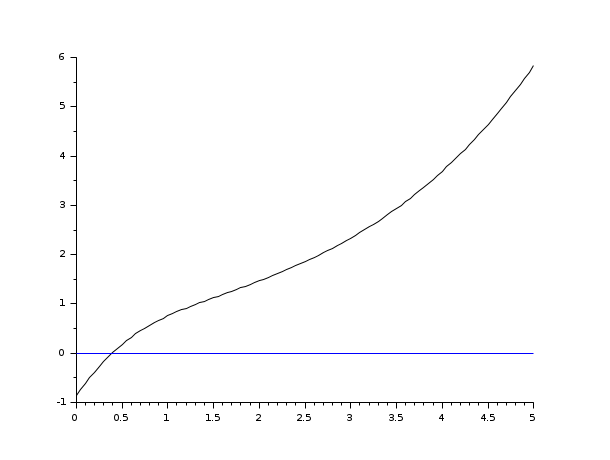
s=poly(0,'s');
rand('seed',0);
w=ssrand(1,1,3);
w('A')=w('A')-2*eye();
t=0:0.05:5;
//step(w) = impulse (s^-1 * w)
plot2d([t',t'],[(csim('step',t,w))',0*t'])

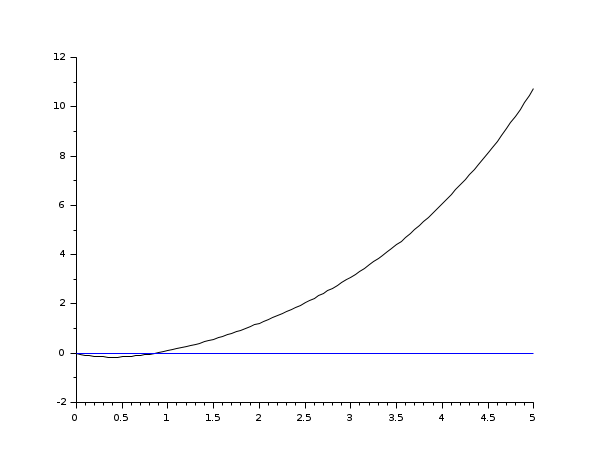
s=poly(0,'s');
rand('seed',0);
w=ssrand(1,1,3);
w('A')=w('A')-2*eye();
t=0:0.05:5;
plot2d([t',t'],[(csim('impulse',t,tf2ss(1/s)*w))',0*t'])

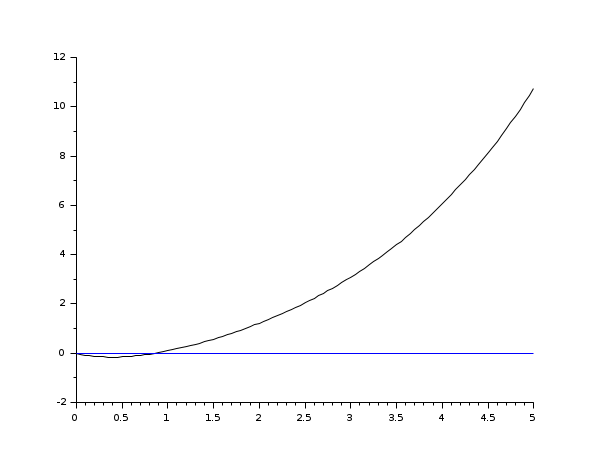
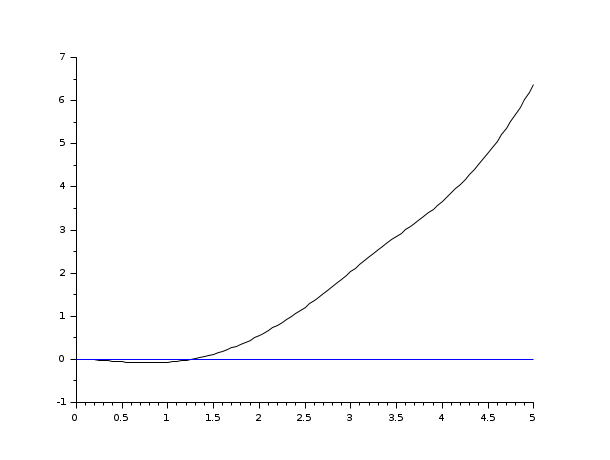
s=poly(0,'s');
rand('seed',0);
w=ssrand(1,1,3);
w('A')=w('A')-2*eye();
t=0:0.05:5;
//input defined by a time function
deff('u=timefun(t)','u=abs(sin(t))')
clf();plot2d([t',t'],[(csim(timefun,t,w))',0*t'])

See Also

• syslin — определение линейной системы
• dsimul — state space discrete time simulation
• flts — time response (discrete time, sampled system)
• ltitr — discrete time response (state space)
• rtitr — discrete time response (transfer matrix)
• ode — программа решения обыкновенных дифференциальных уравнений
• impl — дифференциальное алгебраическое уравнение