Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
高速フーリエ変換
ifft
高速フーリエ逆変換
呼び出し手順
X = fft(A) X = fft(A, sign) X = fft(A, sign, directions) X = fft(A, sign, dims, incr) X = fft(.., symmetry)
パラメータ
- A
- 実数または複素数ベクトル, 実数または複素数配列(ベクトル, 行列またはN-D配列).
- X
Aと同じ形状の実数または複素数配列- sign
- -1 or 1 : sign of the ±2iπ factor in the exponential term inside the
transform formula, setting the direct or inverse transform. The default
value is
-1= Direct transform. - directions
- a vector containing indices of
Adimensions (in [1, ndims(A)]) along which the (multidirectional) FFT must be computed. Default directions=1:ndims(A): The "cumulated" FFT is computed for all directions. See the Description section. - symmetry
- optional character string, helping fft() to choose the best algorithm:
- "symmetric": forces to consider
Aor all its "slices" as conjugate symmetric. This is useful when an exact symmetry ofAor its "slices" is possibly altered only by round-off errors. A N-D arrayBof sizes[s1,s2,..,sN]is conjugate symmetric for the FFT if and only ifB==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). In such a case, the resultXis real, and an efficient specific algorithm can be used to compute it. - "nonsymmetric": Then fft() does not take care of any symmetry.
- not specified: Then an automatic determination of symmetry is performed.
- "symmetric": forces to consider
- dims
- 整数値を有する正の数のベクトルまたは正の整数値のベクトル.
詳細は説明のパートを参照ください.
各要素は
Aの要素の総数の約数とする 必要があります. 要素の積はAの全要素数より 少ない必要があります. - incr
- 整数値を有する正の数のベクトルまたは正の整数値のベクトル.
詳細は説明のパートを参照ください.
incrは,dimsと同じ要素数とする必要があります. 各要素はAの全要素数の約数とする必要があります.incr要素は厳密に昇順とする必要があります.
説明
この関数は直接または逆の1次元またはN次元離散フーリエ変換を 行います.短縮構文
直接
X = fft(A, -1 [,symmetry]) または
X = fft(A [,symmetry]) は直接変換を出力します.
- 単一変量
a=Aが単一変量のベクトルの場合, 次のように直接FFTが計算されます: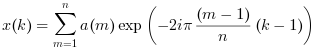
- 多変量
Aが行列または多次元配列の場合, 多変量直接FFTが行われます.
逆
X = fft(A, 1)または X=ifft(A) は,
A == ifft(fft(A))のような 正規化された逆変換を実行します.
- 単一変量
a=Aがベクトルの場合, 単一変量逆FFTが実行されます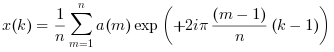
- 多変量
Aが行列または多次元配列の場合, 多変量逆FFTが実行されます.
多次元FFTの長い構文
X = fft(A, sign, directions [, symmetry])
により,選択した次元方向のAの
"スライス"の直接または逆fftを効率的に実行することができます.
例えば,A が3次元配列の場合,
X=fft(A,-1,2)は以下と等価です:
X = fft(A, -1, [1 3])は以下と等価です:
前記の構文,
X = fft(A, sign, dims, incr [, symmetry]) は,
指定した次元方向に Aのスライスの
直接または逆fftを行うことも可能です.
例えば, A が
n1*n2*n3 個の要素を有する配列の場合,
X = fft(A,-1,n1,1) は
X = fft(matrix(A, [n1,n2,n3]), -1, 1)
と等価です.
また、X = fft(A, -1, [n1 n3], [1 n1*n2])
は
X = fft(matrix(A, [n1,n2,n3]), -1, [1,3])
と等価です.
fftの最適化
注意: fftw 関数は自動的に直近のパラメータをメモリに保存し, 2回目に再利用します. これにより,(同じパラメータで)連続的なコールを行った場合に 著しく計算時間が改善します.
get_fftw_wisdom, set_fftw_wisdom関数により 更にfftを最適化することができます.
アルゴリズム: この関数は,fftw3 ライブラリを 使用しています.
参考文献: Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
例
1次元FFT
// Frequency components of a signal // -------------------------------- // build a noised signal sampled at 1000hz containing pure frequencies // at 50 and 70 Hz sample_rate = 1000; t = 0:1/sample_rate:0.6; N = size(t,'*'); // number of samples s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1); y = fft(s); // s is real so the fft response is conjugate symmetric and we retain only the first N/2 points f = sample_rate*(0:(N/2))/N; // associated frequency vector n = size(f,'*') clf() plot(f, abs(y(1:n)))
2次元FFT
//---------------------------------- A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(), "color_map",jetcolormap(128)); clf;grayplot(0:255,0:255,abs(X)')
N-Dimensional FFT:
// simple case, 3 1-D fft at a time N = 2048; t = linspace(0,10,2048); A = [2*sin(2*%pi*3*t)+ sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)]; X = fft(A,-1,2); fs = 1/(t(2)-t(1)); f = fs*(0:(N/2))/N; // associated frequency vector clf; plot(f(1:100)', abs(X(:,1:100))') legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left") // 45 3-D fft at a time Dims = [5 4 9 5 6]; A = matrix(rand(1,prod(Dims)),Dims); y = fft(A,-1,[2 4 5]); // equivalent (but less efficient code) y1 = zeros(A); for i1 = 1:Dims(1) for i3 = 1:Dims(3) ind = list(i1,:,i3,:,:); y1(ind(:)) = fft(A(ind(:)), -1); end end
// Using explicit formula for 1-D discrete Fourier transform // ---------------------------------------------------------- function xf=DFT(x, Sign); n = size(x,'*'); // Compute the n by n Fourier matrix am = exp(Sign*2*%pi*%i*(0:n-1)'*(0:n-1)/n); xf = am*matrix(x,n,1);//dft xf = matrix(xf ,size(x)); // reshape if Sign==1 then xf = xf/n; end endfunction // Comparison with the fast Fourier algorithm a = rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) tic(); DFT(a,-1); toc() tic(); fft(a,-1); toc()
参照
- corr — 相関 , 共分散
- fftw_flags — fftプランナアルゴリズム選択用手法を設定する
- get_fftw_wisdom — fftw wisdomを返す
- set_fftw_wisdom — fftw wisdomを設定
- fftw_forget_wisdom — fftw wisdomをリセット
| Report an issue | ||
| << dst | Transforms | fft2 >> |