Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes

Scilab Online Help
6.1.1 - Português

Scilab-Branch-6.1-GIT

Change language to:
English - Français - 日本語 - Русский

Please note that the recommended version of Scilab is 2025.0.0. This page might be outdated.
See the recommended documentation of this function

Ajuda do Scilab >> Processamento de Sinais > Transforms > fft

fft

Direct or inverse Fast Fourier Transform of a vector, matrix, or hypermatrix

ifft

Inverse fast Fourier transform.

Syntax

X = fft(A)
X = fft(A, sign)
X = fft(A, sign, directions)
X = fft(A, sign, dims, incr)
X = fft(.., symmetry)

Arguments

A, X

vectors, matrices or ND-arrays of real or complex numbers, of same sizes.

sign

-1 or 1 : sign of the ±2iπ factor in the exponential term of the transform formula, setting the direct or inverse transform. The default value is -1 = Direct transform.

directions

vector containing indices of A dimensions (in [1, ndims(A)]) along which the (multidirectional) FFT must be computed. Default directions=1:ndims(A): The "cumulated" FFT is computed for all directions. See the Description section.

symmetry

optional character string, helping fft() to choose the best algorithm:

"symmetric": forces to consider A or all its "slices" as conjugate symmetric. This is useful when an exact symmetry of A or its "slices" is possibly altered only by round-off errors.
A ND-array B of sizes [s1,s2,..,sN] is conjugate symmetric for the FFT if and only if B==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). In such a case, the result X is real, and an efficient specific algorithm can be used to compute it.
"nonsymmetric": Then fft() does not take care of any symmetry.
not specified: Then an automatic determination of symmetry is performed.

dims

vector of positive integers. Old syntax. Each element must be a divisor of length(A). The product of the elements must be strictly smaller than length(A). See the Description section for details.

incr

vector of positive strictly increasing integers, as long as dims. Old syntax. Each element must be a divisor of length(A). See the Description section for details.

Description

This function computes the direct or inverse 1D, 2D, or.. ND Discrete Fourier Transform of an array or ND-array of numbers, along one or several directions inside this one.

Short syntax

Direct transform:

X = fft(A [,symmetry]) or X = fft(A, -1 [,symmetry]) gives a direct transform.

single variate

a=A is a vector: a single variate direct FFT is computed, that is: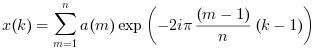

multivariate

A is a matrix or a multidimensional array: A multivariate direct FFT is performed.

Inverse normalized transform:

X = fft(A,+1) or X = ifft(A) performs the inverse normalized transform, such that A==ifft(fft(A)).

single variate

a=A is a vector: X = fft(a, +1) or X = ifft(a) perform a single variate inverse FFT, computed as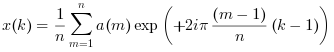

multivariate

A is a matrix or a multidimensional array: A multivariate inverse FFT is performed.

Long syntax : Multidimensionnal directional FFT

X = fft(A, sign, directions [, symmetry]) performs efficiently all direct or inverse FFT of all "slices" of A along selected directions.

For example, if A is a 3D array, X = fft(A,-1,2) is equivalent to:

for i1 = 1:size(A,1)
    for i3 = 1:size(A,3)
        X(i1,:,i3) = fft(A(i1,:,i3), -1);
    end
end

and X = fft(A,-1,[1 3]) is equivalent to:

for i2 = 1:size(A,2)
    X(:,i2,:) = fft(A(:,i2,:), -1);
end

X = fft(A, sign, dims, incr [, symmetry]) is an old syntax that also allows to perform all direct or inverse FFT of the slices of A along selected directions. With this syntax, A is considered as serialized into a vector, and its actual sizes are ignored. The slices are selected by providing A sizes and increments of the serialized index, related to dimensions.

For example, if A is an array with n1*n2*n3 elements, X = fft(A,-1, n1, 1) is equivalent to X = fft(matrix(A,[n1,n2,n3]), -1, 1) ; and X = fft(A,-1, [n1 n3], [1 n1*n2]) is equivalent to X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]).

Optimizing fft

Remark: The fft() function automatically stores its last internal parameters in memory to re-use them in a second time. This improves greatly the time computation when consecutive calls (with same parameters) are performed.

It is possible to go further in fft() optimization using the get_fftw_wisdom and set_fftw_wisdom functions.

Algorithms: fft() uses the fftw3 library.

Bibliography: Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation

Examples

1D FFT (of a vector):

//Frequency components of a signal
//----------------------------------
// build a noised signal sampled at 1000hz  containing  pure frequencies
// at 50 and 70 Hz
sample_rate = 1000;
t = 0:1/sample_rate:0.6;
N = size(t,'*'); //number of samples
s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1);

y=fft(s);

// s is real so the fft response is conjugate symmetric and we retain only the first N/2 points
f = sample_rate*(0:(N/2))/N; //associated frequency vector
n = size(f,'*')
clf()
plot(f, abs(y(1:n)))

2D FFT (of a matrix):

A = zeros(256,256);
A(5:24,13:17) = 1;
X = fftshift(fft(A));
set(gcf(), "color_map",jetcolormap(128));
clf; grayplot(0:255, 0:255, abs(X)')

N-Dimensional FFT (of a ND array):

// simple case, 3 1-D fft at a time
N = 2048;
t = linspace(0,10,2048);
A = [2*sin(2*%pi*3*t) + sin(2*%pi*3.5*t)
     10*sin(2*%pi*8*t)
     sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)];
X = fft(A,-1,2);

fs = 1/(t(2)-t(1));
f = fs*(0:(N/2))/N; // associated frequency vector
clf; plot(f(1:100)',abs(X(:,1:100))')
legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left")

// 45  3-D fft at a time
Dims = [5 4 9 5 6];
A = matrix(rand(1, prod(Dims)), Dims);

y = fft(A,-1,[2 4 5]);

// equivalent (but less efficient code)
y1 = zeros(A);
for i1 = 1:Dims(1)
    for i3 = 1:Dims(3)
        ind = list(i1,:,i3,:,:);
        y1(ind(:)) = fft(A(ind(:)),-1);
  end
end

// Using explicit formula for  1-D discrete Fourier transform
// ----------------------------------------------------------
function xf=DFT(x, Sign);
    n = size(x,'*');
    // Compute the n by n Fourier matrix
    am = exp(Sign * 2*%pi*%i * (0:n-1)'*(0:n-1)/n);
    xf = am * matrix(x,n,1);  // dft
    xf = matrix(xf,size(x));  // reshape
    if Sign == 1 then
        xf = xf/n;
    end
endfunction

// Comparison with the fast Fourier algorithm
a = rand(1,1000);
norm(DFT(a,1) - fft(a,1))
norm(DFT(a,-1) - fft(a,-1))

tic(); DFT(a,-1); toc()
tic(); fft(a,-1); toc()

Report an issue
<< dst	Transforms	fft2 >>

fft