Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
прямое или обратное Быстрое Преобразование Фурье вектора, матрицы или гиперматрицы
ifft
обратное быстрое преобразование Фурье
Синтаксис
X = fft(A) X = fft(A, sign) X = fft(A, sign, directions) X = fft(A, sign, dims, incr) X = fft(.., symmetry)
Аргументы
- A, X
- векторы, матрицы или многомерные массивы вещественных или комплексных чисел одинаковых размеров.
- sign
- -1 или 1 : знак множителя
±2iπв экспоненциальном члене формулы преобразования, устанавливающий прямое или обратное преобразование. По умолчанию значение равно-1, соответствующее прямому преобразованию. - directions
- вектор, содержащий индексы размерности
A(в[1, ndims(A)]) вдоль которой необходимо вычислить БПФ (многомерный). По умолчанию направленияdirectionsсоответствуют1:ndims(A): "кумулятивный" БПФ вычисляется для всех направлений. См. раздел "Описание". - symmetry
- необязательная символьная строка, помогающая функции
fft()выбрать наилучший алгоритм:- "symmetric": заставляет
рассматривать
Aили все её "слои" как симметрично сопряжённую. Это полезно, когда точная симметрияAили её "слоёв" возможно чередуется только из-за ошибок округления. Многомерный массивBразмерами[s1,s2,..,sN]сопряжённо симметричный для БПФ, если и только еслиB==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). В этом случае результатXявляется вещественным и может использоваться эффективный специфический алгоритм для его вычисления. - "nonsymmetric": Тогда
fft()не обращает внимание ни на какую симметрию. - не указано: тогда выполняется автоматическое определение симметрии.
- "symmetric": заставляет
рассматривать
- dims
- вектор положительных целых чисел. Старый синтаксис.
Каждый элемент должен быть делителем
length(A). Произведение элементов должно быть строго меньшеlength(A). См. подробности в разделе "Описание". - incr
- вектор положительных строго возрастающих целых чисел, такой же
длины, что и
dims. Старый синтаксис. Каждый элемент должен быть делителемlength(A). См. подробности в разделе "Описание".
Описание
Эта функция вычисляет прямое или обратное одно-, дву- или многомерное дискретное преобразование Фурье массива или многомерного массива чисел вдоль одного или нескольких направлений внутри этого массива.
Краткий синтаксис
Прямое преобразование:
X = fft(A [,symmetry]) или
X = fft(A, -1 [,symmetry]) выполняет прямое
преобразование.
- одномерное
a=Aявляется вектором: вычисляется одномерное прямое БПФ, так что: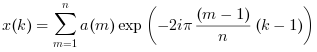
- многомерное
Aявляется матрицей или многомерным массивом: выполняется многомерное прямое БПФ.
Обратное нормированное преобразование:
X = fft(A,+1) или X = ifft(A)
выполняет обратное нормированное преобразование, такое, что
A==ifft(fft(A)).
- одномерное
a=Aявляется вектором:X = fft(a, +1)илиX = ifft(a)выполняют одномерное обратное БПФ, вычисляемое как: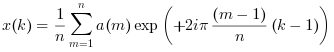
- многомерное
Aявляется матрицей или многомерным массивом: выполняется многомерное обратное БПФ.
Длинный синтаксис: многомерное прямое БПФ
X = fft(A, sign, directions [, symmetry])
выполняет эффективно все прямые или обратные БПФ по всем "слоям"
A вдоль выбранных направлений directions.
Например, если A является трёхмерным массивом, то
X = fft(A,-1,2) эквивалентно:
и X = fft(A,-1,[1 3]) эквивалентно:
X = fft(A, sign, dims, incr [, symmetry])
является старым синтаксисом, который также позволяет выполнять все
прямые или обратные БПФ слоёв A вдоль выбранных
направлений directions. С этим синтаксисом
A рассматривается как сериализованная в вектор, и
её фактические размеры игнорируются. Слои выбираются указанием
размеров A и инкрементов сериализованного индекса,
относящегося к размерам.
Например, если A является массивом с
n1*n2*n3 элементов,
X = fft(A,-1, n1, 1) эквивалентно
X = fft(matrix(A,[n1,n2,n3]), -1, 1) ;
а X = fft(A,-1, [n1 n3], [1 n1*n2])
эквивалентно
X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]).
Оптимизация fft
Примечание:
Функция fft() автоматически сохраняет свои последние
внутренние параметры в памяти для повторного их использования во
второй раз. Это значительно улучшает время вычисления, когда
выполняются последовательные вызовы (с одинаковыми параметрами).
Можно пойти дальше в оптимизации fft(), используя
функции
get_fftw_wisdom и
set_fftw_wisdom.
Алгоритмы:
fft() использует библиотеку
fftw3.
Библиография: Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
Примеры
Одномерное БПФ (вектора):
// Частотные составляющие сигнала //------------------------------- // построение зашумлённого сигнала оцифрованного с частотой 1000 Гц, содержащего чистые // гармоники на 50 и 70 Гц sample_rate = 1000; t = 0:1/sample_rate:0.6; N = size(t,'*'); //количество отсчётов s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1); y=fft(s); // s является вещественным и результат БПФ является сопряжённо симметричным и мы // оставляем только первые N/2 точек f = sample_rate*(0:(N/2))/N; //вектор связанных частот n = size(f,'*') clf() plot(f, abs(y(1:n)))
2D FFT (of a matrix):
A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(), "color_map",jetcolormap(128)); clf; grayplot(0:255, 0:255, abs(X)')
N-мерный БПФ (многомерного массива):
// простой случай, 3 одномерных БПФ во времени N = 2048; t = linspace(0,10,2048); A = [2*sin(2*%pi*3*t) + sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)]; X = fft(A,-1,2); fs = 1/(t(2)-t(1)); f = fs*(0:(N/2))/N; // вектор связанных частот clf; plot(f(1:100)',abs(X(:,1:100))') legend(["3 и 3,5 Гц","8 Гц","0,5 и 0,8 Гц"],"in_upper_left") // 45 трёхмерных БПФ во времени Dims = [5 4 9 5 6]; A = matrix(rand(1, prod(Dims)), Dims); y = fft(A,-1,[2 4 5]); // эквивалентный (но менее эффективный) код y1 = zeros(A); for i1 = 1:Dims(1) for i3 = 1:Dims(3) ind = list(i1,:,i3,:,:); y1(ind(:)) = fft(A(ind(:)),-1); end end
// Использование явной формулы одномерного дискретного преобразования Фурье // ------------------------------------------------------------------------ function xf=DFT(x, Sign); n = size(x,'*'); // вычисление матрицы Фурье размером n на n am = exp(Sign * 2*%pi*%i * (0:n-1)'*(0:n-1)/n); xf = am * matrix(x,n,1); // ДПФ xf = matrix(xf,size(x)); // изменение размерности if Sign == 1 then xf = xf/n; end endfunction // Сравнение с алгоритмом БПФ a = rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) tic(); DFT(a,-1); toc() tic(); fft(a,-1); toc()
Смотрите также
- corr — корреляция, ковариация
- fftw_flags — устанавливают метод вычисления быстрого преобразования Фурье функции fftw
- get_fftw_wisdom — возврат опыта fftw
- set_fftw_wisdom — Устанавливает опыт fftw
- fftw_forget_wisdom — Сброс опыта fftw
| Report an issue | ||
| << dst | transforms | fft2 >> |