Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes

Scilab Online Help
6.1.1 - Français

Scilab-Branch-6.1-GIT

Change language to:
English - 日本語 - Português - Русский

Please note that the recommended version of Scilab is 2025.0.0. This page might be outdated.
See the recommended documentation of this function

Aide de Scilab >> Traitement du Signal > Tranformées > fft

fft

Transformée de Fourier discrète directe ou inverse uni-, bi-, ou N-dimensionnelle

ifft

Transformée de Fourier inverse discrète.

Séquence d'appel

X = fft(A)
X = fft(A, sign)
X = fft(A, sign, directions)
X = fft(A, sign, dims, incr)
X = fft(.., symmetry)

Arguments

A, X

vecteurs, matrices, ou tableaux N-dimensionnels de nombres réels ou complexes, de tailles identiques.

sign

-1 ou 1 = signe du facteur ±2iπ dans le terme exponentiel calculant la transformée, et fixant le sens de celle-ci. Par défaut = -1 = transformée directe.

directions

vecteur contenant les numéros des dimensions A (dans [1, ndims(A)]) selon lesquelles la FFT (multidirectionnelle) doit être calculée. Par défaut, directions=1:ndims(A) : la FFT "cumulée" est calculée pour toutes les directions. Voir la partie "Description" pour plus de détails.

symmetry

mot-texte optionnel, aidant fft() à choisir le meilleur algorithme :

"symmetric": force fft() à considérer A ou toutes ses "tranches" comme symétriques conjuguées. Cela est utile lorsqu'une symétrie exacte attendue a été altérée par des erreurs d'arrondis provenant d'opérations antérieures effectuées sur A.
Un hypertableau numérique N-Dimensionnel B de tailles [s1,s2,..,sN] est conjugué symétrique pur la FFT si et seulement si B==conj(B([1 s1:-1:2],[1 s2:-1:2],...,[1 sN:-1:2])). Dans ce cas, le résultat X est réel. Un algorithme efficace spécifique peut alors être utilisé pour le calculer.
"nonsymmetric": force fft() à ignorer toute propriété de symétrie.
option non fournie : fft() détermine alors automatiquement les propriétés de symétrie de A.

dims

vecteur d'entiers positifs. Chaque élément doit être un diviseur de length(A). Le produit des éléments de dims doit être strictement inférieur à length(A). Ancienne syntaxe. Voir la partie "Description".

incr

vecteur d'entiers positifs strictement croissants, de taille identique à celle de dims. Chaque élément doit être un diviseur de length(A). Ancienne syntaxe. Voir la partie "Description".

Description

Cette fonction calcule la transformée de Fourier discrète directe ou inverse d'un tableau ou d'un hypertableau de nombres, selon une ou plusieurs directions au sein de celui-ci.

Syntaxe courte

Transformée directe :

X = fft(A,-1 [, symmetry]) ou X = fft(A [, symmetry]) calcule la transformée de Fourier discrète directe de A.

monovariable

a=A est un vecteur : x=fft(a,-1) ou x = fft(a) calcule une transformée monovariable, c'est à dire: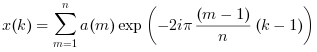

x(k)=∑_m=1…n a(m).exp(-2iπ.(k-1)(m-1)/n)

multivariable

A est une matrice, ou un hypertableau N-dimensionnel : X = fft(A,-1) ou X = fft(A) calcule la transformée de Fourier discrète multivariable directe de A.

Transformée inverse normalisée :

X = fft(A, 1) ou X = ifft(A) calcule la transformée inverse normalisée, telle que A==ifft(fft(A)).

monovariable

a=A est un vecteur : X = fft(a, +1) ou X = ifft(A) calcule la transformée monovariable inverse, c'est à dire :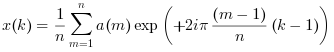

x(k)=(1/n).∑_m=1…n a(m).exp(+2iπ.(k-1)(m-1)/n)

multivariable

A est une matrice ou un hypertableau N-dimensionnel : X = fft(A, +1) ou X = ifft(A) calcule la transformée de Fourier multivariable discrète inverse de A.

Syntaxe longue : FFT directionnelle mutidimensionnelle

X = fft(A, sign, directions [, symmetry]) calcule efficacement les transformées directes ou inverses de toutes les "rangées" de A, selon les directions spécifiées.

Par exemple, si A est un tableau 3D, X = fft(A,-1, 2) est équivalent à

for i1 = 1:size(A,1)
    for i3 = 1:size(A,3)
        X(i1,:,i3) = fft(A(i1,:,i3), -1);
    end
end

et X = fft(A, -1, [1 3]) est équivalent à

for i2 = 1:size(A,2)
    X(:,i2,:) = fft(A(:,i2,:), -1);
end

X = fft(A, sign, dims, incr [, symmetry]) est une syntaxe ancienne qui permet aussi de calculer efficacement les transformées directes ou inverses de "rangées" choisies de A. Avec cette syntaxe, A est vue comme sérialisée en un vecteur, et ses tailles effectives ne sont pas prises en compte. La sélection des "rangées" se fait par la donnée des tailles et des incréments de l'indice sérialisé associés à chacune des dimensions.

Par exemple, si A est un hypertableau ayant n1*n2*n3 éléments, X = fft(A,-1, n1, 1) est équivalent à X = fft(matrix(A,[n1,n2,n3]), -1, 1) ; et X = fft(A, -1, [n1 n3], [1 n1*n2]) est équivalent à X = fft(matrix(A,[n1,n2,n3]), -1, [1,3]).

Optimisation algorithmique de fft()

Remarque : la fonction fft enregistre automatiquement des paramêtres de calcul internes en mémoire (wisdom), pour accélérer les calculs de FFT suivants correspondant aux mêmes directions avec les mêmes options.

Les fonctions get_fftw_wisdom et set_fftw_wisdom permettent de récupérer et de recharger ces paramètres, afin d'améliorer l'efficacité de calcul de FFT lorsqu'on alterne plusieurs types de FFT.

Algorithmes : fft() est basée sur la bibliothèque externe fftw3.

Bibliographie : Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation

Exemples

FFT uni-dimensionnelle (sur un vecteur) :

//Composantes fréquentielles d'un signal
//----------------------------------
// Construction d'un signal bruité échantilloné à 1000hz
//   contenant deux fréquences pures à  50 et 70 Hz.
sample_rate = 1000;
t = 0:1/sample_rate:0.6;
N = size(t,'*'); // nombre d'échantillons
s = sin(2*%pi*50*t) + sin(2*%pi*70*t+%pi/4) + grand(1,N,'nor',0,1);

y = fft(s);
// y est symétrique, on ne garde que  N/2 points
f = sample_rate*(0:(N/2))/N;  // vecteur de fréquences associé
n = size(f,'*')
clf()
plot(f, abs(y(1:n)))

FFT bi-dimensionnelle (sur une matrice)

A = zeros(256,256);
A(5:24,13:17) = 1;
X = fftshift(fft(A));
set(gcf(), "color_map",jetcolormap(128));
clf; grayplot(0:255, 0:255, abs(X)')

FFT ND-dimensionnelle ("hyper-FFT")

// simple case, 3 1-D fft at a time
N = 2048;
t = linspace(0,10,2048);
A = [2*sin(2*%pi*3*t) + sin(2*%pi*3.5*t)
     10*sin(2*%pi*8*t)
     sin(2*%pi*0.5*t) + 4*sin(2*%pi*0.8*t)];
X = fft(A,-1,2);

fs = 1/(t(2)-t(1));
f = fs*(0:(N/2))/N; // associated frequency vector
clf; plot(f(1:100)', abs(X(:,1:100))')
legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left")

// 45  3-D fft at a time
Dims = [5 4 9 5 6];
A = matrix(rand(1,prod(Dims)), Dims);

y = fft(A, -1, [2 4 5]);

// Code équivalent (mais moins efficace)
y1 = zeros(A);
for i1 = 1:Dims(1)
  for i3 = 1:Dims(3)
    ind = list(i1,:,i3,:,:);
    y1(ind(:)) = fft(A(ind(:)), -1);
  end
end

// Définition directe de la transformée de Fourier discrete
// --------------------------------------------------------
function xf=DFT(x, Sign);
    n = size(x,'*');
    // Calcul de la matrice de Fourier (n by n !)
    am = exp(Sign*2*%pi*%i*(0:n-1)'*(0:n-1)/n);
    xf = am*matrix(x,n,1);   // dft
    xf = matrix(xf, size(x)); // mise en forme
    if Sign==1 then
        xf = xf/n
    end
endfunction

// Comparaison avec l'algorithme de la transformée rapide:
a = rand(1,1000);
norm(DFT(a,1) - fft(a,1))
norm(DFT(a,-1) - fft(a,-1))

tic(); DFT(a,-1); toc()
tic(); fft(a,-1); toc()

Voir aussi

corr — correlation, covariance
fftw_flags — choix de la méthode pour la sélection de l'algorithme de planification pour la fft
get_fftw_wisdom — retourne le wisdom fftw
set_fftw_wisdom — charge un wisdom fftw
fftw_forget_wisdom — Réinitialise le wisdom fftw

Report an issue
<< dst	Tranformées	fft2 >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Mon Jan 03 14:33:06 CET 2022