Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
corr
相関 , 共分散
呼び出し手順
[cov,Mean] = corr(x,[y],nlags) [cov,Mean] = corr('fft',xmacro,[ymacro],n,sect) [w,xu] = corr('updt',x1,[y1],w0) [w,xu] = corr('updt',x2,[y2],w,xu) ... wk = corr('updt',xk,[yk],w,xu)
引数
- x
実数ベクトル
- y
実数ベクトル, デフォルト値 x.
- nlags
i整数, 指定した相関係数の数.
- xmacro
scilab 外部ルーチン (下記参照).
- ymacro
scilab 外部ルーチン (下記参照), デフォルト値: xmacro
- n
整数, シーケンス全体の大きさ (下記参照).
- sect
シーケンスのセクションの大きさ (下記参照).
- xi
実数ベクトル
- yi
実数ベクトル,デフォルト値: xi.
- cov
実数ベクトル, 相関係数
- Mean
実数または実数ベクトル, x (および y)の平均
説明
corr(x,y,…) computes
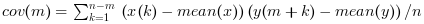 for
for m = 0, …, nlag-1.
シーケンス x および y が異なる場合, corr(x,y,...)はcorr(y,x,...) と異なることに注意してください.
- 短いシーケンス
[cov,Mean]=corr(x,[y],nlags)は, 最初の nlags 個の相関係数および Mean =mean(x)(yが引数として指定された場合,[x,y]の平均) を返します. シーケンスx(またはy) は実数,xとyは同じ次元 n と仮定されます.- 長いシーケンス
[cov,Mean]=corr('fft',xmacro,[ymacro],n,sect)ここで,xmacroは以下のどちらかです[xx]=xmacro(sect,istart)という型の関数で,istartからistart+sect-1までの添字を有するシーケンスの 一部を含むnsect次のベクトルxxを返します.FortranサブルーチンまたはCプロシージャで, 同じ計算を行ないます(例えば,
dgetxの ソースコードを参照ください).
n= シーケンスの総数.sect= シーケンスのセクションの大きさ.sectは 2の累乗とする必要があります.covはsect次です. 計算は FFT により行われます.- 更新法
[w,xu]=corr('updt',x1,[y1],w0) [w,xu]=corr('updt',x2,[y2],w,xu) ... wk=corr('updt',xk,[yk],w,xu)
この呼び出し手順では,計算結果が
corrをコールする度に 更新されます.w0 = 0*ones(1,2*nlags); nlags = power of 2.
x1,x2,...は,x=[x1,x2,...]で,xiの大きさが 2の累乗となるようなxの一部です.nlags個の係数を得るには, 最後の fft をc=fft(w,1)/n;cov=c(1nlags)を実行する必要があります (nはx (y)の大きさ). 注意: この呼び出し手順はxmean = ymean = 0を仮定します.
例
x=%pi/10:%pi/10:102.4*%pi; rand('seed');rand('normal'); y=[.8*sin(x)+.8*sin(2*x)+rand(x);.8*sin(x)+.8*sin(1.99*x)+rand(x)]; c=[]; for j=1:2,for k=1:2,c=[c;corr(y(k,:),y(j,:),64)];end;end; c=matrix(c,2,128);cov=[]; for j=1:64,cov=[cov;c(:,(j-1)*2+1:2*j)];end; rand('normal'); x=rand(1,256);y=-x; deff('[z]=xx(inc,is)','z=x(is:is+inc-1)'); deff('[z]=yy(inc,is)','z=y(is:is+inc-1)'); [c,mxy]=corr(x,y,32); x=x-mxy(1)*ones(x); y=y-mxy(2)*ones(y); //centering c1=corr(x,y,32);c2=corr(x,32); norm(c1+c2,1) [c3,m3]=corr('fft',xx,yy,256,32); norm(c1-c3,1) [c4,m4]=corr('fft',xx,256,32); norm(m3,1),norm(m4,1) norm(c3-c1,1),norm(c4-c2,1) x1=x(1:128); x2=x(129:256); y1=y(1:128); y2=y(129:256); w0=0*ones(1:64); //32 coeffs [w1,xu]=corr('u',x1,y1,w0); w2=corr('u',x2,y2,w1,xu); zz=real(fft(w2,1))/256;c5=zz(1:32); norm(c5-c1,1) [w1,xu]=corr('u',x1,w0); w2=corr('u',x2,w1,xu); zz=real(fft(w2,1))/256;c6=zz(1:32); norm(c6-c2,1) rand('unif') // Fortran または C 外部ルーチンのテスト // deff('[y]=xmacro(sec,ist)','y=sin(ist:(ist+sec-1))'); x=xmacro(100,1); [cc1,mm1]=corr(x,2^3); [cc,mm]=corr('fft',xmacro,100,2^3); [cc2,mm2]=corr('fft','corexx',100,2^3); [max(abs(cc-cc1)), max(abs(mm-mm1)), max(abs(cc-cc2)), max(abs(mm-mm2))] deff('[y]=ymacro(sec,ist)','y=cos(ist:(ist+sec-1))'); y=ymacro(100,1); [cc1,mm1]=corr(x,y,2^3); [cc,mm]=corr('fft',xmacro,ymacro,100,2^3); [cc2,mm2]=corr('fft','corexx','corexy',100,2^3); [max(abs(cc-cc1)), max(abs(mm-mm1)), max(abs(cc-cc2)), max(abs(mm-mm2))]
参照
| Report an issue | ||
| << convol2d | Correlation Convolution | hank >> |