- Scilab Help
- CACSD (Computer Aided Control Systems Design)
- Formal representations and conversions
- Plot and display
- abinv
- arhnk
- arl2
- arma
- arma2p
- arma2ss
- armac
- armax
- armax1
- arsimul
- augment
- balreal
- bilin
- bstap
- cainv
- calfrq
- canon
- ccontrg
- cls2dls
- colinout
- colregul
- cont_mat
- contr
- contrss
- copfac
- csim
- ctr_gram
- damp
- dcf
- ddp
- dhinf
- dhnorm
- dscr
- dsimul
- dt_ility
- dtsi
- equil
- equil1
- feedback
- findABCD
- findAC
- findBD
- findBDK
- findR
- findx0BD
- flts
- fourplan
- freq
- freson
- fspec
- fspecg
- fstabst
- g_margin
- gamitg
- gcare
- gfare
- gfrancis
- gtild
- h2norm
- h_cl
- h_inf
- h_inf_st
- h_norm
- hankelsv
- hinf
- imrep2ss
- inistate
- invsyslin
- kpure
- krac2
- lcf
- leqr
- lft
- lin
- linf
- linfn
- linmeq
- lqe
- lqg
- lqg2stan
- lqg_ltr
- lqr
- ltitr
- macglov
- minreal
- minss
- mucomp
- narsimul
- nehari
- noisegen
- nyquistfrequencybounds
- obs_gram
- obscont
- observer
- obsv_mat
- obsvss
- p_margin
- parrot
- pfss
- phasemag
- plzr
- pol2des
- ppol
- prbs_a
- projsl
- repfreq
- ric_desc
- ricc
- riccati
- routh_t
- rowinout
- rowregul
- rtitr
- sensi
- sident
- sorder
- specfact
- ssprint
- st_ility
- stabil
- sysfact
- syslin
- syssize
- time_id
- trzeros
- ui_observer
- unobs
- zeropen
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
arl2
SISO model realization by L2 transfer approximation
Calling Sequence
h=arl2(y,den0,n [,imp]) h=arl2(y,den0,n [,imp],'all') [den,num,err]=arl2(y,den0,n [,imp]) [den,num,err]=arl2(y,den0,n [,imp],'all')
Arguments
- y
real vector or polynomial in
z^-1, it contains the coefficients of the Fourier's series of the rational system to approximate (the impulse response)- den0
a polynomial which gives an initial guess of the solution, it may be
poly(1,'z','c')- n
integer, the degree of approximating transfer function (degree of den)
- imp
integer in
(0,1,2)(verbose mode)- h
transfer function
num/denor transfer matrix (column vector) when flag'all'is given.- den
polynomial or vector of polynomials, contains the denominator(s) of the solution(s)
- num
polynomial or vector of polynomials, contains the numerator(s) of the solution(s)
- err
real constant or vector , the l2-error achieved for each solutions
Description
[den,num,err]=arl2(y,den0,n [,imp]) finds a pair of polynomials
num and den such that the transfer function num/den
is stable and its impulse response approximates (with a minimal l2
norm) the vector y assumed to be completed by an infinite number
of zeros.
If y(z) = y(1)(1/z)+y(2)(1/z^2)+ ...+ y(ny)(1/z^ny)
then l2-norm of num/den - y(z) is err.
n is the degree of the polynomial den.
The num/den transfer function is a L2 approximant of the
Fourier's series of the rational system.
Various intermediate results are printed according to imp.
[den,num,err]=arl2(y,den0,n [,imp],'all') returns in the
vectors of polynomials num and den a set of local
optimums for the problem. The solutions are sorted with increasing
errors err. In this case den0 is already assumed to be
poly(1,'z','c')
Examples
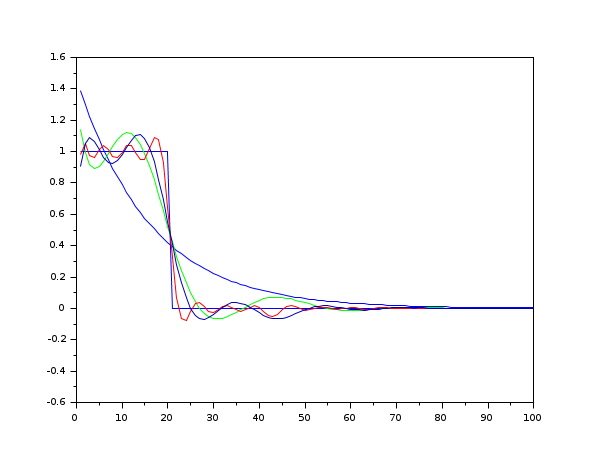
v=ones(1,20); clf(); plot2d1('enn',0,[v';zeros(80,1)],2,'051',' ',[1,-0.5,100,1.5]) [d,n,e]=arl2(v,poly(1,'z','c'),1) plot2d1('enn',0,ldiv(n,d,100),2,'000') [d,n,e]=arl2(v,d,3) plot2d1('enn',0,ldiv(n,d,100),3,'000') [d,n,e]=arl2(v,d,8) plot2d1('enn',0,ldiv(n,d,100),5,'000') [d,n,e]=arl2(v,poly(1,'z','c'),4,'all') plot2d1('enn',0,ldiv(n(1),d(1),100),10,'000')
See Also
| Report an issue | ||
| << arhnk | CACSD (Computer Aided Control Systems Design) | arma >> |