Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
nchoosek
Computes binomial numbers (n,k) = numbers of combinations
Syntax
b = nchoosek(n, k) logb = nchoosek(n, k, logFormat) [logb, b] = nchoosek(n, k, logFormat) [logb, b] = nchoosek(n, k)
Arguments
- n, k
- arrays of positive decimal integers. If both
nandkare not scalars, they must have the same size. - b
- array of positive decimal integers, with the size of the biggest array
nork: Cnk - logb
- array of positive decimal numbers, with the size of
b:log10(Cnk) - logFormat
- single word "log10" | "10.mant". "log10" by default.
- If "log10" is used,
logbreturnslog10(b). - If "10.mant" is used, then
logbreturnsint(log10(b)) + 10^(log10(b)-int(log10(b)))/10: The 10-exponent of b is the logb integer part, while its fractional part directly shows the mantissa/10 of b, in [1.0, 10)/10.
- If "log10" is used,
Description
For every (n(i),k(i)) element-wise pair, nchoosek() computes the number of
ki-element subsets of an ni-element set.
It is mathematically defined by
![C(n,k) = n! / [ k! (n-k)! ]](/docs/6.1.1/pt_BR/_LaTeX_nchoosek.xml_1.png) .
The implementation, though, uses the βeta function.
.
The implementation, though, uses the βeta function.
If n < 0, or k < 0, or k > n, then an error is generated.
Note about floating point accuracy
Despite n! overflows for n>170, nchoosek(n,k) is computed within almost the %eps relative accuracy for n much beyond 170.
For any given n value, we know that Cnk is maximal for k=n/2. Scilab computes b = nchoosek(n,n/2) close to the %eps relative accuracy for n up to 1029. Beyond this value, b=%inf is returned.
This narrow n=1029 limit can be overcome by computing log10(Cnk) and returning it through the second output argument logb. This allows to use still bigger n values, and to get some valid information about the exponent and the mantissa of the true result.
However, we must keep in mind that beyond n = 1/%eps ~ 4.1015,
the numerical step between consecutive integers m and m+1 stored as floating point
numbers become > 1. Then n*(n-1) is numerically equal to
n*n, and getting reliable results becomes harder.
The integer part of logb represents the exponent (of 10) of Cnk, whereas its fractional part is the log10 of its mantissa. When the integer part of logb increases, the more digits it takes among the 16 available ones in floating point encoding, the less remain to encode the mantissa. Then, knowing the mantissa of Cnk with at least one significant digit requires Cnk < 101014.
Relative accuracy on logb: As a rule of thumb, except for special k cases, the relative uncertainty on logb is of the order of %eps * n / k.
Examples
Simple examples
c = nchoosek(4, 1) c = nchoosek(5, 0) c = nchoosek([4 5], [1 0])
--> c = nchoosek(4, 1) c = 4. --> c = nchoosek(5, 0) c = 1. --> c = nchoosek([4 5], [1 0]) c = 4. 1.
nchoosek(10, 0:10) nchoosek(4:12, 4)
--> nchoosek(10, 0:10) ans = 1. 10. 45. 120. 210. 252. 210. 120. 45. 10. 1. --> nchoosek(4:12, 4) ans = 1. 5. 15. 35. 70. 126. 210. 330. 495.
For big values:
exact = 2.050083865033972676e307; c = nchoosek(10000, 134) relerror = abs(c-exact)/exact
--> c = nchoosek(10000, 134) c = 2.05D+307 --> relerror = abs(c-exact)/exact relerror = 7.959D-14
The exact result for
Cnk(n, 2) is
n.(n-1)/2. Now, for values n > 1/%eps = 4e15,
(n-1) is numerically identical to n. In no way
we can expect an exact result below, but rather n^2/2 :
n = 1e20; c = nchoosek(n, 2) c / (n*n/2) - 1 // Relative error wrt the expected numerical value
--> c = nchoosek(n, 2) c = 5.000D+39 --> c /(n*n/2) - 1 ans = -6.661D-15
In logarithmic formats:
[logb, b] = nchoosek(10000, 1234); [b, logb] logb = nchoosek(10000, 1234, "10.mant") [logb, b] = nchoosek(1000, 500); logb2 = nchoosek(1000, 500, "10.mant"); [b, logb, logb2] logb = nchoosek(1000, 500, "log10")
--> [logb, b] = nchoosek(10000, 1234); [b, logb] ans = Inf 1620.803261 --> logb = nchoosek(10000, 1234, "10.mant") logb = 1620.635713 // 6.35713D+1620 --> [logb, b] = nchoosek(1000, 500); --> logb2 = nchoosek(1000, 500, "10.mant"); --> [b, logb, logb2] ans = 2.7029D+299 299.4318272 299.2702882 --> logb = nchoosek(1000, 500, "log10") logb = 299.4318272
Drawing nchoosek(n,k) on the main floating point domain, up to
10300 :
function ax=drawCnk(n) // Preparing data [N,K] = meshgrid(n); noOp = K>N; K(noOp) = 0; [logC, C] = nchoosek(N, K); C(noOp) = %nan; if max(n)<2000, logC = log10(C), end // Surface of Cnk data surf(N, K, logC); gce().color_mode = -2; // hidding the mesh plot2d([0 n],[0 n/2]); gce().children.data(:,3) = max(logC(logC<>%inf)) // Axes settings xgrid(25,1,7) ax = gca(); set(ax, "view","2d", "tight_limits",["on" "on" "off"], "grid_position","foreground"); xtitle("","","",""); ax.margins(2) = 0.05; // Color bar colorbar(); cb = gce(); cb.y_ticks.labels = msprintf("$\\Large 10^{%s}$\n", cb.y_ticks.labels); title(cb,"$C_n^k$", "fontsize",3) endfunction clf drawlater // Figure settings f = gcf(); f.color_map = jetcolormap(100); //f.axes_size = [840 570]; // Main plot ax = drawCnk(0:10:1500); sca(ax); xtitle("nchoosek(n, k)","n","k","$C_n^k$"); set([ax.title ax.x_label ax.y_label ax.z_label], "font_size",4); xstring(1250, 450, "Overflow") gce().font_size = 4; // Inset xsetech([0.11 0.11 0.37 0.42]); ax = drawCnk(0:106); ax.sub_ticks = [3 3]; gce().sub_ticks(2) = 4; drawnow
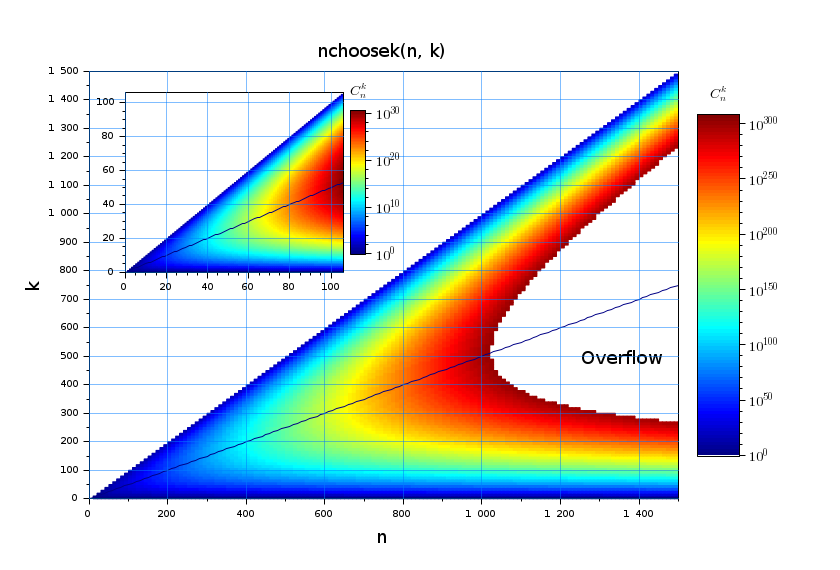
Going beyond, in logarithmic mode :
// /!\ : The drawCnk() function used here is defined in the previous example. clf drawlater // Figure settings f = gcf(); f.color_map = jetcolormap(100); //f.axes_size = [840 570]; // Main plot ax = drawCnk(0:10000:1e6); sca(ax); xtitle("nchoosek(n, k)","n","k","$C_n^k$"); set([ax.title ax.x_label ax.y_label ax.z_label], "font_size",4); // Inset xsetech([0.12 0.11 0.37 0.42]); ax = drawCnk(0:1000:1e5); ax.sub_ticks = [3 3]; gce().sub_ticks(2) = 4; drawnow
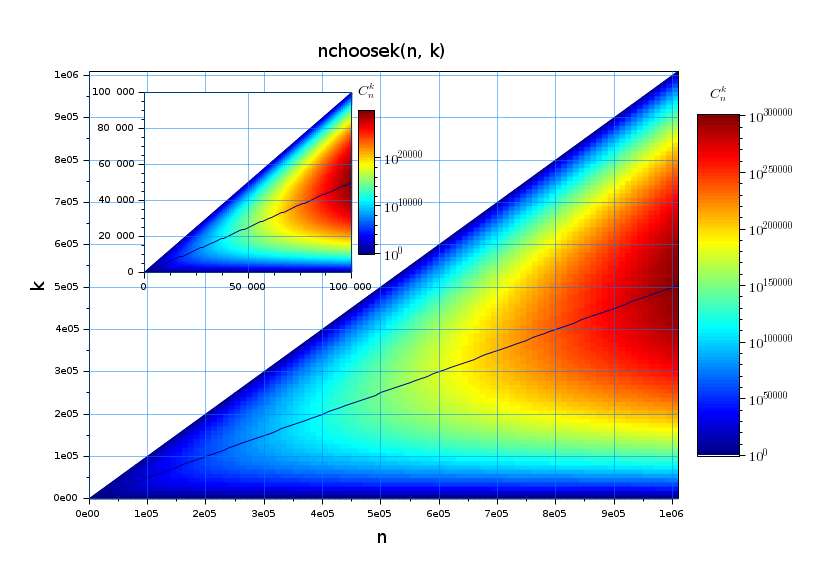
Top line Cnn/2 :
nchoosek(n, n/2) and its known close approximation
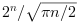
n = round(10^(1:0.1:8))*2; logb = nchoosek(n, n/2, "log10"); clf plot2d("ll", n, logb) ax = gca(); xgrid(color("grey70"), 1, 7); //ax.sub_ticks = [ 8 0]; ax.tight_limits = "on"; ax.y_ticks.labels = msprintf("$\\Large 10^{%d}$\n", ax.y_ticks.locations); xlabel("n", "fontsize",4); xstring(60, 1000, "nchoosek(n, n/2)", 270) set(gce(), "clip_state", "off", "font_size",3); // Relative difference with the 2^n / sqrt(pi.n/2) approximation: e = abs(10.^(n*log10(2) - (log10(%pi)+log10(n/2))/2 - logb) - 1); ax = newaxes(); ax.filled = "off"; ax.y_location = "right"; ax.tight_limits = ["on" "off"]; ax.font_color = color("magenta"); plot2d("ll", n, e, style=color("magenta")) ax.axes_visible(1) = "off"; legend("$\large \left|{\frac{2^n}{\sqrt{\pi n/2}} / nchoosek(n, n/2)}-1\right|$", .. "in_upper_left", %f);
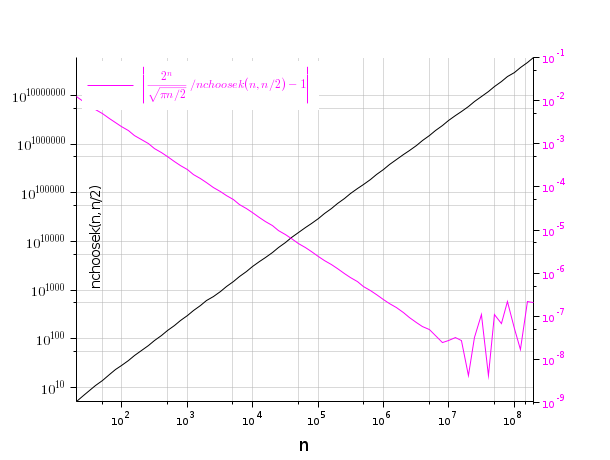
Bibliography
- Binomial coefficients (Wikipedia)
- Boost C++ librairies, Binomial Coefficients, 2006 , 2007, 2008, 2009, 2010 : John Maddock, Paul A. Bristow, Hubert Holin, Xiaogang Zhang, Bruno Lalande, Johan Råde, Gautam Sewani and Thijs van den Berg.
- "Introduction to discrete probabilities with Scilab", Michael Baudin, 2010
See also
History
| Versão | Descrição |
| 6.1.0 | nchoosek() introduced. |
| Report an issue | ||
| << lcm | Matemática discreta | primes >> |