sysdiag

設定

ai

サブシステム (すなわち,ゲインまたは状態空間表現または 伝達関数表現の線形システム)

任意の大きさの定数, 論理値, 多項式または有理数行列

r

a1, a2, a3, ... を対角項に有する行列

説明

sysdiag() is obsolete. Please use blockdiag() instead.

主対角項にサブシステムを配置したブロック対角システムを返します.

入力A, B および Cを指定すると, 出力はこれらの行列を以下のように対角項に配置したものになります:

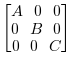
入力行列が全て正方の場合, 出力は ブロック対角行列として 知られたものになります.

特にシステムの相互接続で使用されます.

論理値行列の場合,sysdiag() は常に 対応するブロックに 0 または 1を要素とする行列 ("true"値は1,"false"値は0で置換されます)を返します.

注意

引数の数は最大17個に制限されています.

例

s = poly(0,'s')
sysdiag(rand(2,2),1/(s+1),[1/(s-1);1/((s-2)*(s-3))])
sysdiag(tf2ss(1/s),1/(s+1),[1/(s-1);1/((s-2)*(s-3))])

// a matrix of doubles:
A = [1 0; 0 1], B=[3 4 5; 6 7 8], C=7
D = sysdiag(A,B,C)
//
sysdiag([%t %f; %f %t], eye(2,2), ones(3,3))
// a polynomial matrix:
s = %s;
sysdiag([s 4*s; 4 s^4], [1 s^2 s+2; 3*s 2 s^2-1])
// a rational matrix:
sysdiag([1/s 2*s/(4*s+3)], [s; 4; 1/(s^2+2*s+1)])
// a block diagonal sparse matrix:
S = sysdiag([1 2; 3 4], [5 6; 7 8], [9 10; 11 12], [13 14; 15 16])
S = sparse(S)

参照

• diag — 対角行列の構築または展開
• bdiag — ブロック対角化, 一般化固有ベクトル
• repmat — 配列を複製/タイル状に配置
• brackets — Concatenation. Recipients of an assignment. Results of a function
• feedback — フィードバック操作

履歴