lqi

Linear quadratic integral compensator (full state)

Syntax

[K,X]=lqi(P,Q,R [,S])

Arguments

P: The plant state space representation (see syslin) with nx states, nu inputs and ny outputs.
Q: Real nx+ny by nx+ny symmetric matrix,
R: full rank nu by nu real symmetric matrix
S: real nx+ny by nu matrix, the default value is zeros(nx+ny,nu)
K: a real matrix, the optimal gain
X: a real symmetric matrix, the stabilizing solution of the Riccati equation

Description

This function computes the linear quadratic integral full-state gain K for the plant P. The associated system block diagram is:

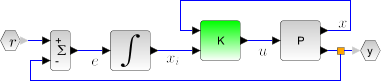
The plant P is given by its state space representation

The cost function in l2-norm is:

where

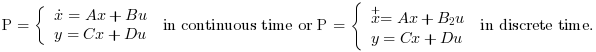
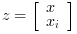and

is the integrator(s) state(s);

Algorithm

The lqi function solves the lqr problem for the augmented plant

Caution

It is assumed that matrix 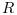is non singular.

Remark

If the full state of the system is not available, An estimator of the plant state can be built using the lqe function.

Examples

Linear quadratic integral controller of a simplified disk drive using state observer.

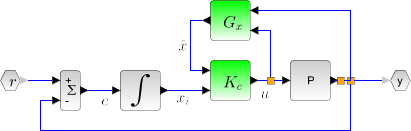
//Disk drive model
G=syslin("c",[0,32;-31.25,-0.4],[0;2.236068],[0.0698771,0]);
t=linspace(0,20,2000);
y=csim("step",t,G);

//State estimator
Wy=1;
Wu=1;
S=0;
Q=G.B*Wu*G.B';
R=Wy+G.D*S + S'*G.D+G.D*Wu*G.D';
S=G.B*Wu*G.D'+S;

//State estimator
[Kf,X]=lqe(G,Q,R,S);
Gx=observer(G,Kf);

//LQI compensator

wy=100;
Q= wy*sysdiag(G.C'*G.C,1);
R=1/wy;
Kc=lqi(G,Q,R);
//full controller
K=lft([1;1]*(-Kc(1:2)*Gx(:,[2 1])+Kc(3)*[1/%s 0]),1);//e-->u

//Full system
H=(-K*G)/.(1);// full system transfer function

y=csim("step",t,H);
clf;plot(t,y)

Report an issue
<< lqg_ltr	Linéaire Quadratique	lqr >>

lqi