Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
lqg2stan
LQG to standard problem
Syntax
[P_aug,r]=lqg2stan(P,Qxu,Qwv)
Arguments
- P22
State space representation of the nominal plant (
nuinputs,nyoutputs,nxstates).- Qxu
[Q,S;S',N]symmetricnx+nubynx+nuweighting matrix.- Qwv
[R,T;T',V]symmetricnx+nybynx+nycovariance matrix.- r
Row vector
[ny nu].- P_aug
Augmented plant state space representation (see: syslin)
Description
lqg2stan returns the augmented plant for linear LQG (H2) controller
design problem defined by:
The nominal plant
P22:described by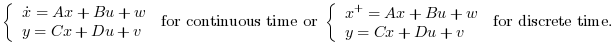
The (instantaneous) cost function
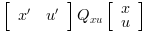 .
.The noises covariance matrix
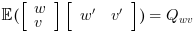
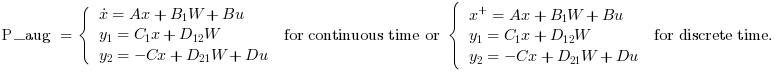
 | Up to Scilab-5.5.2 lqg2stan returns wrong inverted values
(see bug 13751)
to obtain the good result one had to use This bug is fixed since Scilab-6.0.0, old codes must be modified accordingly. |
Algorithm
If [B1;D21] is a factor of
Qxu, [C1,D12] is a
factor of Qwv (see: fullrf) then
P_aug=syslin(P.dt,P.A,[B1,P.B],[C1;-P.C],[0,D12;D21,P.D])
Examples
ny=2;nu=3;nx=4; P22=ssrand(ny,nu,nx); Qxu=rand(nx+nu,nx+nu);Qxu=Qxu*Qxu'; Qwv=rand(nx+ny,nx+ny);Qwv=Qwv*Qwv'; [P_aug,r]=lqg2stan(P,Qxu,Qwv); K=lqg(P_aug,r); //K=LQG-controller spec(h_cl(P_aug,r,K)) //Closed loop should be stable //Same as Cl=P22/.K; spec(Cl('A')) s=poly(0,'s') lqg2stan(1/(s+2),eye(2,2),eye(2,2))
See also
- lqg — LQG compensator
- lqr — LQ compensator (full state)
- lqe — linear quadratic estimator (Kalman Filter)
- obscont — observer based controller
- h_inf — Continuous time H-infinity (central) controller
- augment — augmented plant
- fstabst — Youla's parametrization of continuous time linear dynamical systems
- feedback — feedback operation
| Report an issue | ||
| << lqg | Linéaire Quadratique | lqg_ltr >> |