引数

zu

大きさMの列ベクトル. 複数の点で指定したメッシュ上で評価したODEの解. 各点における z(u(x)) が含まれます.

xpoints

解を観測する点を指定する配列.

N

整数値を有するスカラー,微分方程式の数 (N <= 20).

m

整数要素を有する大きさ N のベクトル. mは各微分方程式の次数のベクトルで, m(i)はi番目の微分方程式の次数を指定します. 以下に示す Mは mの要素の合計を表します.

x_low

スカラー: 区間の左端

x_up

スカラー: 区間の右端

zeta

大きさ Mのベクトル,zeta(j) は, j番目の端の条件点(境界値)を指定します. x_low<=zeta(j) <= zeta(j+1)<=x_up となります.

全ての境界条件点は, 使用される全てのメッシュにおけるメッシュ点とする必要があります. 以下の ipar(11) および fixpntの説明を参照ください.

ipar

11個の整数要素を有する配列:

[nonlin, collpnt, subint, ntol, ndimf, ndimi, iprint, iread, iguess, rstart,nfxpnt]

nonlin: ipar(1)

問題が線形の場合: 0 ,問題が非線形の場合: 1

collpnt: ipar(2)

サブ区間毎のコロケーション点の数を指定します. ただし, where max(m(j)) <= collpnt <= 7

ipar(2)=0 の場合, collpnt は ( max(m(j))+1 , 5-max(m(j)) )に設定されます

subint: ipar(3)

初期メッシュのサブ区間の数を指定します. ipar(3) = 0 の場合, 適宜 subint = 5と設定します.

ntol: ipar(4)

解と微分の許容誤差の数を指定します. 0 < ntol <= M とする必要があります. ipar(4) は, tol 引数の次元または 0に設定する必要があります. 後者の場合, 実際の値は自動的に size(tol,'*') に設定されます.

ndimf: ipar(5)

fspace(実数の作業配列)の次元を指定します. この値は, サブ区間の最大数 nmax への拘束条件を指定します.

ipar(5) の値は,拘束条件 ipar(5)>=nmax*nsizef を考慮する必要があります. ただし

nsizef=4+3*M+(5+collpnt*N)*(collpnt*N+M)+(2*M-nrec)*2*M (nrec は終端境界条件の数です ).

ndimi: ipar(6)

ispace (整数作業配列)の次元を指定します. この値は, サブ区間の最大数 nmax への拘束条件を指定します.

ipar(6) の値は, 拘束条件 ipar(6)>=nmax*nsizei を考慮する必要があります. ただし,

nsizei=3 + collpnt*N+M.

iprint: ipar(7)

出力制御, 以下の値とします:

-1

完全な診断出力の場合

0

部分的な出力の場合

1

出力しない場合

iread: ipar(8)

= 0

bvodeが一様な初期メッシュを生成するようにします.

= xx

他の値は, Scilabでは未実装です.

= 1

初期メッシュがユーザにより指定される場合. fspace で以下のように定義されます:

メッシュは fspace(1), ..., fspace(n+1) となります. ユーザは内部メッシュ点fspace(j) = x(j), j = 2, ..., n. のみを指定する必要があります.

= 2 初期メッシュがユーザにより指定される場合.

ipar(8)=1が指定された時と同様であり, 加えて,適応型メッシュ選択は行われません.

iguess: ipar(9)

= 0

解の初期推定値が指定されない場合.

= 1

引数 guess により, 初期推定値がユーザにより指定される場合.

= 2

初期メッシュと近似解係数がユーザにより fspace で指定される場合 (前のメッシュと新規メッシュは同じものになります).

= 3

前のメッシュと近似解の係数がユーザによりfspace で指定される場合, 新規メッシュは 2倍荒くとられます. すなわち, 前のメッシュの各2点毎に1点となります．

= 4

前の初期メッシュと近似解係数に加えて,同時に 新規メッシュが fspace に出力されます. (詳細はiguess = 2, 3, および 4の出力の説明を参照ください)

ireg: ipar(10)

= 0

問題が標準の場合

= 1

最初の緩和係数が ireg に等しい場合, 非線形反復は過去の収束結果に基づきません. (別の敏感な非線形問題のみで使用されます)

= 2

以下の場合,直ちにリターンします. (a) 2回連続で収束しない場合, または (b)最初に誤差推定値を得た後.

nfxpnt: ipar(11)

x_low および x_up 以外のメッシュの固定点の数(fixpntの次元)を指定します. ipar(11) は,引数 fixpntの次元または 0に設定する必要があります. 後者の場合, 実際の値は自動的に size(fixpnt,'*') に設定されます.

ltol

次元 ntol=ipar(4)の配列. ltol(j) = l は, tol 配列の j番目の許容誤差を指定します.これは, 以下のl番目の要素の誤差を制御します.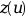 .以下も必要です:

1 <= ltol(1) < ltol(2) < ... < ltol(ntol) <= M

tol

ntol=ipar(4)次の配列.

tol(j)は, 以下の ltol(j) 番目の要素の許容誤差です.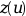 .つまり, このコードは以下の条件を 満たそうとします. 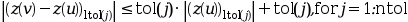(サブ区間について)

が近似解ベクトルの場合, 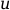は厳密解(未知)となります.

fixpnt

nfxpnt=ipar(11)次の配列. 各メッシュに含まれるx_low および x_up以外の点を含みます. このコードは,x_low および x_up 以外の全ての周辺条件点(zetaの説明を参照)が fixpntの中の固定点として 含まれることを必要とします.

fsub

external は,以下の 列ベクトルの評価に使用されます. f=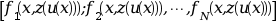 ただし, x_low <= x <= x_up の任意のx, および z=z(u(x)) となる任意のz とします. (以下の説明を参照)

外部関数は以下のように宣言を必要とします:

• Fortranの場合, 呼び出し手順を以下のようにします:

  subroutine fsub(x,zu,f)
  double precision zu(*), f(*),x

• Cの場合,関数プロトタイプを以下のようにします:

  void fsub(double *x, double *zu, double *f)

• そしてScilab上では:

  function f=fsub(x, zu, parameters)

dfsub

externalは, 点xにおけるヤコビアンf(x,z(u))の 評価に使用されます. ただし,z(u(x))は, fsubと同様に定義され, N 行 M列配列 dfには,fの偏微分が代入されます: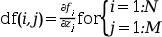

外部関数は以下のように宣言を必要とします:

• Fortranの場合, 呼び出し手順を以下のようにします:

  subroutine dfsub(x,zu,df)
  double precision zu(*), df(*),x

• Cの場合, 関数プロトタイプを以下のようにします:

  void dfsub(double *x, double *zu, double *df)

• そして,Scilabにおいては:

  function df=dfsub(x, zu, parameters)

gsub

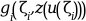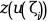
以下の評価に使用されるexternal given z= z = zeta(i) ただし, 1<=i<=M.

外部関数は以下のように宣言を必要とします:

• Fortranの場合, 呼び出し手順を以下のようにします:

  subroutine gsub(i,zu,g)
  double precision zu(*), g(*)
  integer i

• Cの場合, 関数プロトタイプを以下のようにします:

  void gsub(int *i, double *zu, double *g)

• そして,Scilabでは:

  function g=gsub(i, zu, parameters)

  fsubのfとは逆に gでは コール毎に一つの値のみが返されることに注意してください.

dgsub

an external used to evaluate the i-th row of the Jacobian of g(x,u(x)). Where z(u) is as for fsub, i as for gsub and the M-vector dg should be filled with the partial derivatives of g, viz, for a particular call one calculates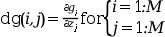

外部関数は以下のような宣言を必要とします:

• Fortranの場合, 呼び出し手順を以下のようにします:

  subroutine dgsub(i,zu,dg)
  double precision zu(*), dg(*)

• Cの場合, 関数プロトタイプを以下のようにします:

  void dgsub(int *i, double *zu, double *dg)

• そして,Scilabでは:

  function dg=dgsub(i, zu, parameters)

guess

z(u(x))および u(x)のmj階微分dmval(u(x)) の初期近似値を見積もるために externalが使用されます. ipar(9) = 1の場合のみ, このサブルーチンが 使用されることに注意してください. このため，zuのM個の要素および dmval の N個の 要素がx_low <= x <= x_upの範囲の任意の x について計算される 必要があります.

外部関数は以下のように宣言を必要とします:

• Fortranの場合, 呼び出し手順を以下のようにします:

  subroutine guess(x,zu,dmval)
  double precision x,z(*), dmval(*)

• Cの場合, 関数プロトタイプを以下のようにします

  void fsub(double *x, double *zu, double *dmval)

• そしてScilab上では,

  function [dmval, zu]=fsub(x, parameters)

<optional_args>

以下のどれかとする必要があります:

• 以下の一連の値: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol,nonlin, collpnt, subint, iprint, ireg, ifail

• もしくは,一連のarg_name=argvalue で指定します. ただし arg_name は以下のどれかとなります: guess, dfsub, dgsub, fixpnt, ndimf, ndimi, ltol, tol, ntol, nonlin, collpnt, subint, iprint, ireg, ifail

これらの引数が指定される場合は,常に ifailは上記のように説明されます. ifailは選択されたオプション引数 に対応する bvode コールを表示するために使用できます. もし，guess が指定された場合, iguessが 1 に設定されます.

説明

これらの関数は, 以下のように定義された ode-s の 混合次数に関連するシステム多点境界値問題を解きます.

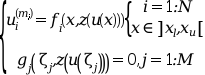
ただし,e

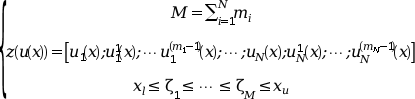
外部関数で使用され, bvode により返される 引数 zu は, 指定した x に関する z(u(x))の要素により 構成される列ベクトルです.

解 u を近似するために使用される手法は, ガウス点におけるコロケーションです. この方法は,i番目(i = 1:N)の要素についてm(i)-1階の連続微分が可であることを 必要とします. ここで, k はサブ区間毎のコロケーション点(ステージ)の数で, 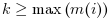となるように選択されます. ルンゲクッタのノミナル解表現が使用されます.

例

最初の2つの問題は参考文献の論文 [1] からの引用です.

• 問題 1 は 両端で単純支持され,均等に負荷がかかった剛性が可変の梁について 記述します.

  以下のように定義することができます :

  次の4次の微分方程式を解きます:

  

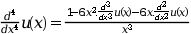
  設定する境界条件:

  

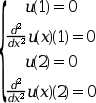
  この問題の厳密解は以下のようになることが知られています:

  

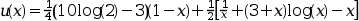
  N=1;// just one differential equation
  m=4;//a fourth order  differential equation
  M=sum(m);
  
  x_low=1;x_up=2; // the x limits
  zeta=[x_low,x_low,x_up,x_up]; //two constraints (on the value of u and its second derivative) on each bound.
  
  //The external functions
  //These functions are called by the solver with zu=[u(x);u'(x);u''(x);u'''(x)]
  
  // - The function which computes the right hand side of the differential equation
  function f=fsub(x, zu),f=(1-6*x^2*zu(4)-6*x*zu(3))/x^3,endfunction
  
  // - The function which computes the derivative of fsub with respect to zu
  function df=dfsub(x, zu),df=[0,0,-6/x^2,-6/x],endfunction
  
  // - The function which computes the ith constraint for a given i
  function g=gsub(i, zu),
    select i
    case 1 then  //x=zeta(1)=1
      g=zu(1) //u(1)=0
    case 2 then //x=zeta(2)=1
      g=zu(3) //u''(1)=0
    case 3 then //x=zeta(3)=2
      g=zu(1) //u(2)=0
    case 4 then  //x=zeta(4)=2
      g=zu(3) //u''(2)=0
    end
  endfunction
  
  // - The function which computes the derivative of gsub with respect to z
  function dg=dgsub(i, z)
    select i
    case 1 then  //x=zeta(1)=1
      dg=[1,0,0,0]
    case 2 then //x=zeta(2)=1
      dg=[0,0,1,0]
    case 3 then //x=zeta(3)=2
       dg=[1,0,0,0]
    case 4 then  //x=zeta(4)=2
      dg=[0,0,1,0]
    end
  endfunction
  
  // - The function which computes the initial guess, unused here
  function [zu, mpar]=guess(x),zu=0;mpar=0,endfunction 
  
   //define the function which computes the exact value of u for a given x ( for testing purposes)
  function zu=trusol(x)
    zu=0*ones(4,1)
    zu(1) =  0.25*(10*log(2)-3)*(1-x) + 0.5 *( 1/x   + (3+x)*log(x) - x)
    zu(2) = -0.25*(10*log(2)-3)       + 0.5 *(-1/x^2 + (3+x)/x      + log(x) - 1)
    zu(3) = 0.5*( 2/x^3 + 1/x   - 3/x^2)
    zu(4) = 0.5*(-6/x^4 - 1/x/x + 6/x^3)
  endfunction
  
  fixpnt=[ ];//All boundary conditions are located at x_low and x_up
  
  //    nonlin  collpnt n ntol ndimf  ndimi iprint iread iguess rstart nfxpnt
  ipar=[0       0       1 2    2000   200   1      0     0      0      0     ]
  
  ltol=[1,3];//set tolerance control on zu(1) and zu(3)
  tol=[1.e-11,1.e-11];//set tolreance values for these two controls
  xpoints=x_low:0.01:x_up;
  
  zu=bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
          fsub,dfsub,gsub,dgsub,guess)
  //check the constraints
  zu([1,3],[1 $]) //should be zero
  plot(xpoints,zu(1,:)) // the evolution of the solution u
  zu1=[];for x=xpoints,zu1=[zu1,trusol(x)]; end;  
  norm(zu-zu1)

• 同じ問題で bvodeS と初期推定を用います

  function [z, lhS]=zstart(x)
    z=zeros(5,1);z(5)=1;
    lhS=[0;1];
  endfunction
  zu=bvode(xpoints,N,m,x_low,x_up,zeta,ltol=ltol,tol=tol,guess=zstart)

• 問題 2は, 二次関数として変化する軸対象の外部圧力分布のもとでの 一定の厚みの薄く浅い球状のキャップの 微小な有限変形を記述するものです. ここで, 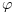は変形したシェルの経線角度変化, 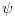は応力関数です. 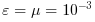の場合,開始点に依存して2つの異なる解が得られる可能性が あります.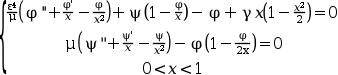

  

  境界条件のもとで

  

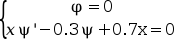
  x=0 かつ x=1の場合

  N=2;// two differential equations
  m=[2 2];//each differential equation is of second  order
  M=sum(m);
  
  x_low=0;x_up=1; // the x limits
  zeta=[x_low,x_low, x_up x_up]; //two  constraints on each bound.
  
  //The external functions
  //These functions are called by the solver with zu=[u1(x);u1'(x);u2(x);u2'(x)]
  
  // - The function which computes the right hand side of the differential equation
  function f=fsub2(x, zu, eps, dmu, eps4mu, gam, xt),
     f=[zu(1)/x^2-zu(2)/x+(zu(1)-zu(3)*(1-zu(1)/x)-gam*x*(1-x^2/2))/eps4mu //phi''
        zu(3)/x^2-zu(4)/x+zu(1)*(1-zu(1)/(2*x))/dmu];//psi''
  endfunction
  
  // - The function which computes the derivative of fsub with respect to zu
  function df=dfsub2(x, zu, eps, dmu, eps4mu, gam, xt),
    df=[1/x^2+(1+zu(3)/x)/eps4mu, -1/x, -(1-zu(1)/x)/eps4mu, 0
        (1-zu(1)/x)/dmu             0    1/x^2              -1/x];
  endfunction
  
  // - The function which computes the ith constraint for a given i
  function g=gsub2(i, zu),
    select i
    case 1 then  //x=zeta(1)=0
      g=zu(1) //u(0)=0
    case 2 then //x=zeta(2)=0
      g=-0.3*zu(3) //x*psi'-0.3*psi+0.7x=0
    case 3 then //x=zeta(3)=1
      g=zu(1) //u(1)=0
    case 4 then  //x=zeta(4)=1
      g=1*zu(4)-0.3*zu(3)+0.7*1 //x*psi'-0.3*psi+0.7x=0
    end
  endfunction
  
  // - The function which computes the derivative of gsub with respect to z
  function dg=dgsub2(i, z)
    select i
    case 1 then  //x=zeta(1)=1
      dg=[1,0,0,0]
    case 2 then //x=zeta(2)=1
      dg=[0,0,-0.3,0]
    case 3 then //x=zeta(3)=2
       dg=[1,0,0,0]
    case 4 then  //x=zeta(4)=2
      dg=[0,0,-0.3,1]
    end
  endfunction
  
  gam=1.1
  eps=1d-3
  dmu=eps
  eps4mu=eps^4/dmu
  xt=sqrt(2*(gam-1)/gam)
  
  fixpnt=[ ];//All boundary conditions are located at x_low and x_up
  collpnt=4;
  nsizef=4+3*M+(5+collpnt*N)*(collpnt*N+M)+(2*M-2)*2*M ;
  nsizei=3 + collpnt*N+M;;
  nmax=200;
  //    nonlin  collpnt n  ntol ndimf        ndimi        iprint iread iguess rstart nfxpnt
  ipar=[1       k       10 4    nmax*nsizef  nmax*nsizei   -1      0     0      0      0     ]
  
  ltol=1:4;//set tolerance control on zu(1), zu(2), zu(3) and zu(4)
  tol=[1.e-5,1.e-5,1.e-5,1.e-5];//set tolreance values for these four controls
  xpoints=x_low:0.01:x_up;
  
  zu=bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
          fsub2,dfsub2,gsub2,dgsub2,guess2);
  scf(1);clf();plot(xpoints,zu([1 3],:)) // the evolution of the solution phi and psi
  
  //using an initial guess
  // - The function which computes the initial guess, unused here
  function [zu, dmval]=guess2(x, gam),
     cons=gam*x*(1-x^2/2)
     dcons=gam*(1-3*x^2/2)
     d2cons=-3*gam*x
     dmval=zeros(2,1)
     if x>xt then
       zu=[0 0 -cons -dcons]
       dmval(2)=-d2cons
     else
       zu=[2*x;2;-2*x+cons;-2*dcons]
       dmval(2)=d2cons
     end
  endfunction 
  ipar(9)=1;//iguess
  
  zu2=bvode(xpoints,N,m,x_low,x_up,zeta,ipar,ltol,tol,fixpnt,...
          fsub2,dfsub2,gsub2,dgsub2,guess2);
  scf(2);clf();plot(xpoints,zu2([1 3],:)) // the evolution of the solution phi and psi

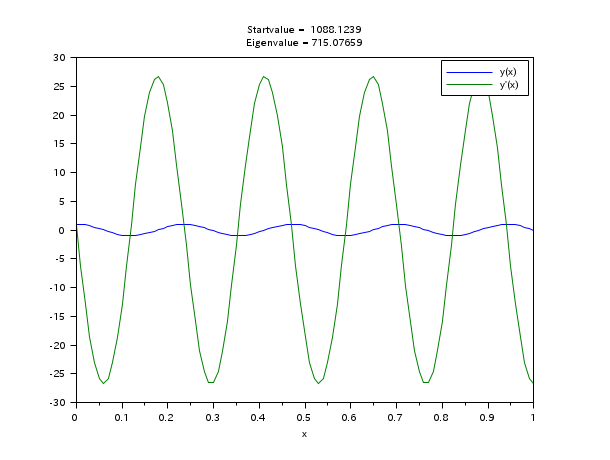
• 固有値問題:

  // y''(x)=-la*y(x)
  // BV: y(0)=y'(0); y(1)=0
  // Eigenfunctions and eigenvalues are y(x,n)=sin(s(n)*(1-x)), la(n)=s(n)^2,
  // where s(n) are the zeros of f(s,n)=s+atan(s)-(n+1)*pi, n=0,1,2,...
  // To get a third boundary condition, we choose y(0)=1
  // (With y(x) also c*y(x) is a solution for each constant c.)
  // We solve the following ode system:
  // y''=-la*y
  // la'=0
  // BV: y(0)=y'(0), y(0)=1; y(1)=0
  // z=[y(x) ; y'(x) ; la]
  
  function rhs=fsub(x, z)
    rhs=[-z(3)*z(1);0]
  endfunction
  
  function g=gsub(i, z)
    g=[z(1)-z(2) z(1)-1 z(1)]
    g=g(i)
  endfunction
  
  // The following start function is good for the first 8 eigenfunctions.
  function [z, lhs]=ystart(x, z, la0)
    z=[1;0;la0]
    lhs=[0;0]
  endfunction
  
  a=0;b=1;
  m=[2;1];
  n=2;
  zeta=[a a b];
  N=101;
  x=linspace(a,b,N)';
  
  // We have s(n)-(n+1/2)*pi -> 0 for n to infinity.
  la0=input('n-th eigenvalue: n= ?');la0=(%pi/2+la0*%pi)^2;
  
  z=bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,la0));
  
  clf()
  plot(x,[z(1,:)' z(2,:)']) 
  xtitle(['Startvalue =  '+string(la0);'Eigenvalue = '+string(z(3,1))],'x',' ')
  legend(['y(x)';'y''(x)'])

  

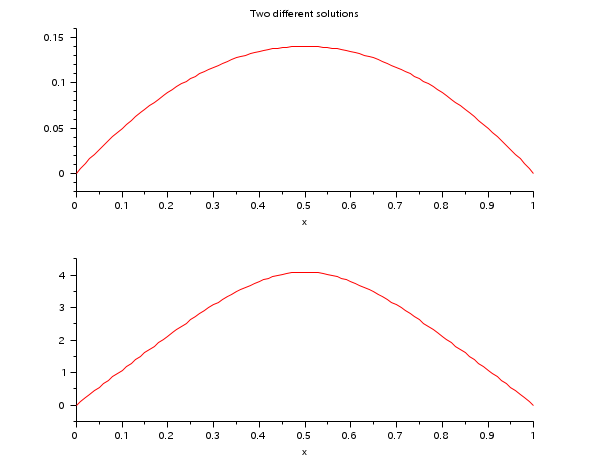
• 複数の解がある多点境界値問題.

  // DE: y''(x)=-exp(y(x))
  // BV: y(0)=0; y(1)=0
  // This boundary value problem has more than one solution.
  // It is demonstrated how to find two of them with the help of
  // some preinformation of the solutions y(x) to build the function ystart.
  // z=[y(x);y'(x)]
  
  a=0;b=1;m=2;n=1;
  zeta=[a b];
  N=101;
  tol=1e-8*[1 1];
  x=linspace(a,b,N);
  
  function rhs=fsub(x, z),rhs=-exp(z(1));endfunction
  
  function g=gsub(i, z)
    g=[z(1) z(1)]
    g=g(i)
  endfunction
  
  function [z, lhs]=ystart(x, z, M) 
    //z=[4*x*(1-x)*M ; 4*(1-2*x)*M]
    z=[M;0]
    //lhs=[-exp(4*x*(1-x)*M)]
    lhs=0
  endfunction
  
  for M=[1 4]
     if M==1
        z=bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,M),tol=tol);
     else
        z1=bvodeS(x,m,n,a,b,fsub,gsub,zeta,ystart=list(ystart,M),tol=tol);
     end
  end
  
  // Integrating the ode yield e.g. the two solutions yex and yex1. 
  
  function y=f(c),y=c.*(1-tanh(sqrt(c)/4).^2)-2;endfunction 
  c=fsolve(2,f);
  
  function y=yex(x, c)
    y=log(c/2*(1-tanh(sqrt(c)*(1/4-x/2)).^2))
  endfunction 
  
  function y=f1(c1), y=2*c1^2+tanh(1/4/c1)^2-1;endfunction
  c1=fsolve(0.1,f1);
  
  function y=yex1(x, c1)
    y=log((1-tanh((2*x-1)/4/c1).^2)/2/c1/c1)
  endfunction 
  
  disp(norm(z(1,:)-yex(x)),'norm(yex(x)-z(1,:))= ')
  disp(norm(z1(1,:)-yex1(x)),'norm(yex1(x)-z1(1,:))= ')
  clf();
  subplot(2,1,1)
  plot2d(x,z(1,:),style=[5])
  xtitle('Two different solutions','x',' ') 
  subplot(2,1,2)
  plot2d(x,z1(1,:),style=[5])
  xtitle(' ','x',' ')

  

• 多点境界値問題.

  // DE y'''(x)=1
  // z=[y(x);y'(x);y''(x)]
  // BV: y(-1)=2 y(1)=2
  // Side condition: y(0)=1 
  
  a=-1;b=1;c=0;
  // The side condition point c must be included in the array fixpnt.
  n=1;
  m=[3];
  
  function rhs=fsub(x, z)
    rhs=1
  endfunction
  
  function g=gsub(i, z)
    g=[z(1)-2 z(1)-1 z(1)-2]
    g=g(i)
  endfunction
  
  N=10;
  zeta=[a c b];
  x=linspace(a,b,N);
  
  z=bvodeS(x,m,n,a,b,fsub,gsub,zeta,fixpnt=c);
            
  function y=yex(x)
  y=x.^3/6+x.^2-x./6+1
  endfunction
  
  disp(norm(yex(x)-z(1,:)),'norm(yex(x)-z(1,:))= ')

• 2個の "固有値" (c_1 および c2)を有するQuantum Neumann方程式. 連続法を使用します.

  // Quantum Neumann equation, with 2 "eigenvalues" c_1 and c_2
  // (c_1=v-c_2-c_3, v is a parameter, used in continuation)
  //
  // diff(f,x,2) + (1/2)*(1/x + 1/(x-1) + 1/(x-y))*diff(f,x)
  //      - (c_1/x + c_2/(x-1) + c_3/(x-y))* f(x) = 0
  // diff(c_2,x)=0,  diff(c_3,x) = 0
  //
  // and 4 "boundary" conditions: diff(f,x)(a_k)=2*c_k*f(a_k) for
  // k=1,2,3, a_k=(0, 1 , y)  and normalization f(1) = 1
  //
  // The z-vector is z_1=f, z_2=diff(f,x), z_3=c_2 and z_4=c_3
  // The guess is chosen to have one node in [0,1],  f(x)=2*x-1
  // such that f(1)=1, c_2 and c_3 are chosen to cancel poles in
  // the differential equation at 1.0 and y, z_3=1, z_4=1/(2*y-1)
  // Ref: http://arxiv.org/pdf/hep-th/0407005
  
  y= 1.9d0;
  eigens=zeros(3,40); // To store the results
  
  // General setup for bvode
  
  // Number of differential equations
  ncomp = 3;
  
  // Orders of equations
  m = [2, 1, 1];
  
  // Non-linear problem
  ipar(1) = 1;
  
  // Number of collocation points
  ipar(2) = 3;
  
  // Initial uniform mesh of 4 subintervals
  ipar(3) = 4;
  ipar(8) = 0;
  
  // Size of fspace, ispace, see colnew.f to choose size
  ipar(5) =  30000;
  ipar(6) =  2000;
  
  // Medium output
  ipar(7) = 0;
  
  // Initial approx is provided
  ipar(9) = 1;
  
  // fixpnt is an array containing all fixed points in the mesh, in
  // particular "boundary" points, except aleft and aright, ipar[11] its
  // size, here only one interior "boundary point"
  ipar(11) = 1;
  fixpnt = [1.0d0];
  
  // Tolerances on all components z_1, z_2, z_3, z_4
  ipar(4) = 4;
  
  // Tolerance check on f and diff(f,x) and on c_2 and c_3
  ltol = [1, 2, 3, 4];
  tol = [1d-5, 1d-5, 1d-5, 1d-5];
  
  // Define the differential equations
  
  function [f]=fsub(x, z)
      f = [ -.5*(1/x+1/(x-1)+1/(x-y))*z(2) +...
       z(1) * ((v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y)),...
      0,0];
  endfunction
  function [df]=dfsub(x, z)
      df = [(v-z(3)-z(4))/x + z(3)/(x-1) + z(4)/(x-y),...
      -.5*(1/x+1/(x-1)+1/(x-y)),z(1)/(x*(x-1)),z(1)*y/(x*(x-y));...
      0,0,0,0;0,0,0,0];
  endfunction
  
  // Boundary conditions
  
  function [g]=gsub(i, z)
      select i
      case 1, g = z(2) - 2*z(1)*(v-z(3)-z(4))
      case 2, g = z(2) - 2*z(1)*z(3)
      case 3, g = z(1)-1.
      case 4, g = z(2) - 2*z(1)*z(4)
      end
  endfunction
  function [dg]=dgsub(i, z)
          select i
          case 1, dg = [-2*(v-z(3)-z(4)),1.,2*z(1),2*z(1)]
          case 2, dg = [-2*z(3),1.,-2*z(1),0]
          case 3, dg = [1,0,0,0]
          case 4, dg = [-2*z(4),1.,0,-2*z(1)]
          end
  endfunction
  
  // Start computation
  
  // Locations of side conditions, sorted
  zeta = [0.0d0, 1.0d0, 1.0d0, y];
  // Interval ends
  aleft = 0.0d0;
  aright = y;
  
  // Array of 40 values of v explored by continuation, and array of 202
  // points where to evaluate function f.
  valv = [linspace(0,.9,10) logspace(0,2,30)];
  res = [linspace(0,.99,100) linspace(1,y,101)];
  
  // eigenstates are characterized by number of nodes in [0,1] and in
  // [1,y], here guess selects one node (zero) in [0,1] with linear
  // f(x)=2*x-1 and constant c_2, c_3, so dmval=0. Notice that the z-vector
  // has mstar = 4 components, while dmval has ncomp = 3 components.
  
  function [z, dmval]=guess(x)
       z=[2*x-1, 2., 1., 1/(2*y-1)]
       dmval=[0,0,0]
  endfunction
  
  // First execution has ipar(9)=1 and uses the guess
  // Subsequent executions have ipar(9)=3 and use continuation. This is
  // run in tight closed loop to not disturb the stack
  
  for i=1:40
  v=valv(i);
  sol=bvode(res,ncomp,m,aleft,aright,zeta,ipar,ltol,tol,fixpnt,...
   fsub,dfsub,gsub,dgsub,guess);
  eigens(:,i)=[v;sol(3,101);sol(4,101)];  // c_2 and c_3 are constant!
  ipar(9)=3;
  end
  
  // To see the evolution of the eigenvalues with v, disp(eigens)
  // Note they evolve smoothly.
  // To see the solution f for v=40, disp(sol(1,:)). Note that it vanishes
  // exactly once in [0,1] at x close to 0.98, and becomes very small
  // when x -> 0 and very large when x -> y.
  // This is markedly different from the case  at small v.
  // The continuation procedure allows to explore these exponential behaviours
  // without skipping to other eigenstates.

参照

• link — dynamic linker
• external — Scilabオブジェクト, 外部関数またはルーチン
• ode — 常微分方程式ソルバ
• dassl — 微分代数方程式

使用される関数

この関数は, 以下の作者により開発された Fortran ルーチンcolnew に基づいています.

U. Ascher, Department of Computer Science, University of British Columbia, Vancouver, B.C. V6T 1W5, Canada

G. Bader, institut f. Angewandte mathematik university of Heidelberg; im Neuenheimer feld 294d-6900 Heidelberg 1

参考文献

1. U. Ascher, J. Christiansen and R.D. Russell, collocation software for boundary-value ODEs, acm trans. math software 7 (1981), 209-222. this paper contains EXAMPLES where use of the code is demonstrated.

2. G. Bader and U. Ascher, a new basis implementation for a mixed order boundary value ode solver, siam j. scient. stat. comput. (1987).

3. U. Ascher, J. Christiansen and R.D. Russell, a collocation solver for mixed order systems of boundary value problems, math. comp. 33 (1979), 659-679.

4. U. Ascher, J. Christiansen and R.D. russell, colsys - a collocation code for boundary value problems, lecture notes comp.sc. 76, springer verlag, b. childs et. al. (eds.) (1979), 164-185.

5. C. Deboor and R. Weiss, solveblok: a package for solving almost block diagonal linear systems, acm trans. math. software 6 (1980), 80-87.