Scilab 5.3.0
- Manuel Scilab
- Fonctions Elémentaires
- Mathématiques discrètes
- Virgule flottante
- Représentation d'entier
- Trigonométrie
- abs
- amell
- and
- &
- cumprod
- cumsum
- delip
- diag
- exp
- eye
- gsort
- imag
- intersect
- inttrap
- isdef
- isreal
- kron
- lex_sort
- linspace
- log
- log10
- log2
- logm
- logspace
- lstsize
- max
- meshgrid
- min
- modulo
- norm
- ones
- or
- |
- pen2ea
- prod
- rand
- real
- resize_matrix
- sign
- signm
- size
- solve
- sqrt
- sqrtm
- squarewave
- sum
- syslin
- toeplitz
- trianfml
- tril
- trisolve
- triu
- union
- unique
- zeros
- binomial
- bitand
- bitor
- bloc2exp
- bloc2ss
- cat
- cell2mat
- cellstr
- char
- diff
- dsearch
- flipdim
- imult
- ind2sub
- isempty
- isequal
- isequalbitwise
- isvector
- log1p
- ndgrid
- ndims
- nextpow2
- permute
- pertrans
- setdiff
- ssrand
- sub2ind
- sysconv
- sysdiag
- trfmod
- typeof
- vectorfind
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
binomial
binomial distribution probabilities
Calling Sequence
pr=binomial(p,n)
Arguments
- pr
row vector with n+1 components
- p
real number in [0,1]
- n
an integer >= 1
Description
pr=binomial(p,n) returns the binomial probability
vector, i.e. pr(k+1) is the probability of
k success in n independent
Bernouilli trials with probability of success p. In
other words : pr(k+1) = probability(X=k) , with X a
random variable following the B(n,p) distribution, and numerically
:
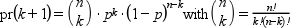
Examples
// first example n=10;p=0.3; clf(); plot2d3(0:n,binomial(p,n)); // second example n=50;p=0.4; mea=n*p; sigma=sqrt(n*p*(1-p)); x=( (0:n)-mea )/sigma; clf() plot2d(x, sigma*binomial(p,n)); deff('y=Gauss(x)','y=1/sqrt(2*%pi)*exp(-(x.^2)/2)') plot2d(x, Gauss(x), style=2); // by binomial formula (Caution if big n) function pr=binomial2(p, n) x=poly(0,'x');pr=coeff((1-p+x)^n).*horner(x^(0:n),p); endfunction p=1/3;n=5; binomial(p,n)-binomial2(p,n) // by Gamma function: gamma(n+1)=n! (Caution if big n) p=1/3;n=5; Cnks=gamma(n+1)./(gamma(1:n+1).*gamma(n+1:-1:1)); x=poly(0,'x'); pr=Cnks.*horner(x.^(0:n).*(1-x)^(n:-1:0),p); pr-binomial(p,n)
| << zeros | Fonctions Elémentaires | bitand >> |