kinsol
SUNDIALS general-purpose nonlinear system solver
Syntax
[y,val,info,extra] = kinsol(f,y0,options)
Arguments
| f | a function, a string or a list, the right hand side of the nonlinear system |
| y0 | a double array: initial guess |
| options | a sequence of optional named arguments, see the solvers options |
| y,val | double arrays: approximate solution at the end of solver iterations and value of the system function, at y, respectively |
| info | an integer, the solver exit code, see the related section below |
| extra | a MList containing solver information and statistics, see the related section below |
Description
kinsol computes the solution of a real or complex system of nonlinear algebraic equations under the classical form
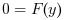
or under the fixed-point form
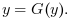
It is an interface to kinsol solver of SUNDIALS library with default inexact Newton method for classical form or fixed-point iterations with Anderson acceleration for fixed-point form. The solver has a specific feature which allows to constrain the sign of solution components (see the options page). Unlike the native implementation, the Scilab interface allows to solve the system when the function and/or solution is complex (see the Complex solutions help page).
In its simplest form, the solver call takes the form
y = kinsol(f,y0)
where y0 is the
initial guess, y is the
approximate solution yielded by the solver given default tolerance (which can be changed in options).
The right hand side can be computed by a Scilab function with one argument, but if you need to pass extra parameters and/or want to
use DLL entrypoints see the user functions help page.
Example
In the following example, we solve the following system of equations
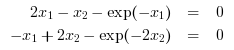
with the initial guess [0,0], default inexact Newton method and display solver iterations:
PDE example
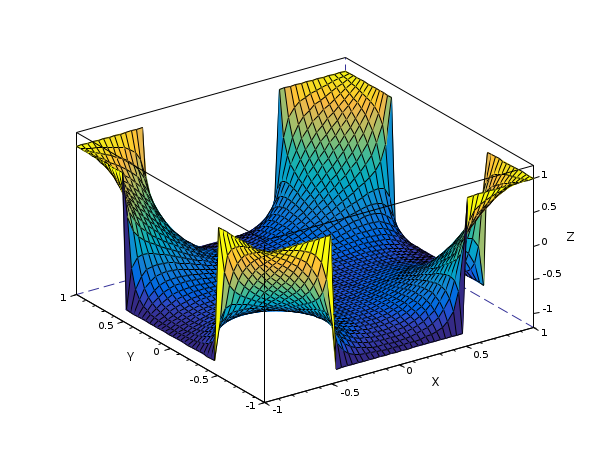
In the following example, we approximate the solution of the following nonlinear pde
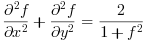
with finite differences, on [-1,1]x[-1,1] and a particular nonhomogeneous Dirichlet boundary condition. The band Jacobian is approximated with finite differences.
function out=fun(f, lap, bdy) out = lap*f - 2./(1+f.*f) out(bdy) = f(bdy)-sign(cos(%pi*(X(bdy)+Y(bdy)))); endfunction // define square domain [-1,1] x [-1,1] n = 50; x=linspace(-1,1,n); y=x; [X,Y]=meshgrid(x,x); // build Laplacian operator dx=x(2)-x(1); d1x=sparse(ones(n-1,1)); d0x=sparse(ones(n,1)); lap = (diag(d1x,-1)+diag(d1x,1)-2*diag(d0x))/dx/dx; // use Kronecker product to build matrix of d/dx^2 and d/dy^2 LAP = lap .*. speye(n,n) + speye(n,n) .*. lap; // Find boundary nodes BDY = find(X(:)==x(1) | X(:)==x($) | Y(:)==y(1) | Y(:)==y($))'; f = kinsol(list(fun,LAP,BDY),ones(n*n,1), jacBand=[n,n], display="iter"); clf gcf().color_map=parula(128); surf(x,x,matrix(f,n,n))
Exit codes
| 0 | Successful function return |
| 1 | The initial user-supplied guess already satisfies the stopping criterion |
| 2 | The stopping tolerance on scaled step length was satisfied |
| -5 | The linesearch algorithm was unable to find an iterate sufficiently distinct from the current iterate |
| -6 | The maximum number of nonlinear iterations has been reached |
| -7 | Five consecutive steps have been taken that satisfy a scaled step length test |
| -99 | The solver has been stopped by user callback |
Extra output and statistics
The extra optional output argument is a MList with fields:
| solver | the solver name, "kinsol" | ||||||||||||||||
| method | the name of the method used by the solver: "Newton" (inexact Newton method), "lineSearch" (inexact Newton method with linesearch globalization), "Picard" (Picard iterations), and "fixedPoint" (fixed-point iterations) | ||||||||||||||||
| linearSolver | the linear solver used by the method, if applicable. This field is "none" when using fixed-point iterations. In other cases this field can be "dense", "band" or "sparse" depending on the format of the Jacobian provided by the user. | ||||||||||||||||
| stats | a structure gathering the solver statistics:
|
See also
- User functions — Coding user functions used by SUNDIALS solvers
- Options (kinsol) — Changing the default behavior of solver
Bibliography
A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S. Woodward, "SUNDIALS: Suite of Nonlinear and Differential/Algebraic Equation Solvers," ACM Transactions on Mathematical Software, 31(3), pp. 363-396, 2005. Also available as LLNL technical report UCRL-JP-200037.
Alan C. Hindmarsh and Radu Serban and Cody J. Balos and David J. Gardner and Daniel R. Reynolds and Carol S. Woodward, "User Documentation for kinsol, 2021, v6.1.1, available online at https://sundials.readthedocs.io/en/latest/kinsol
| Report an issue | ||
| << ida | SUite of Nonlinear and DIfferential/ALgebraic equation - SUNDIALS solvers | bvode >> |