fchamp
direction field of a 2D first order ODE
Syntax
fchamp(f, t, xr, yr, [arfact, rect, strf]) fchamp(f, t, xr, yr, <opt_args>)
Arguments
- f
an external (function or character string) or a list which describes the ODE.
- -
It can be a function name
f, wherefis supposed to be a function of typey=f(t, xy, [p1, ..., pn]).freturns a column vector of size 2,y, which gives the value of the direction fieldfat pointxy=[x,y]and at timet.- -
It can also be an object of type list,
list(f,P1, ..., Pn)wherefis a function of typey=f(t, xy, p1, ..., pn)andPigives the value of the parameterpi.
- t
the selected time.
- xr, yr
two row vectors of size
n1andn2which define the grid on which the direction field is computed.- <opt_args>
This represents a sequence of statements
key1=value1, key2=value2,... wherekey1,key2,... can be one of the following:arfact,rect,strf(see below).- arfact, rect, strf
Optional arguments, see
champ.
Description
fchamp is used to draw the direction field of a
2D first order ODE defined by the external function
f.
 | Note that if the ODE is autonomous, argument
t is useless, but it must be given. |
Enter the command fchamp() to see a demo.
Examples
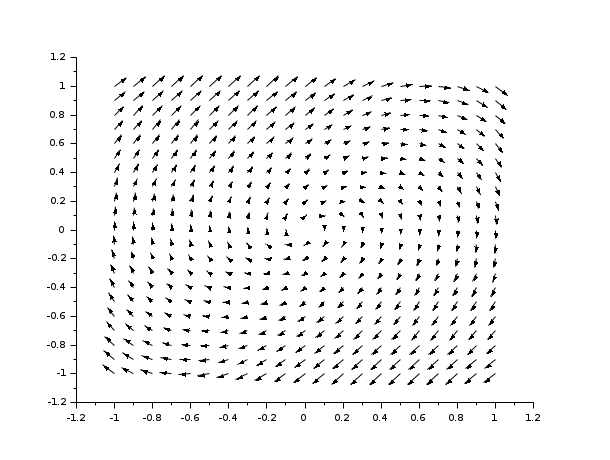
deff("[xdot] = derpol(t,x)",.. ["xd1 = x(2)";.. "xd2 = -x(1) + (1 - x(1)**2)*x(2)";.. "xdot = [ xd1 ; xd2 ]"]) xf= -1:0.1:1; yf= -1:0.1:1; fchamp(derpol,0,xf,yf)
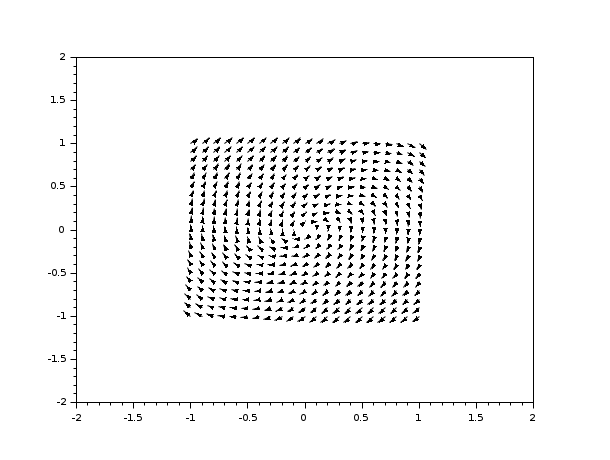
deff("[xdot] = derpol(t,x)",.. ["xd1 = x(2)";.. "xd2 = -x(1) + (1 - x(1)**2)*x(2)";.. "xdot = [ xd1 ; xd2 ]"]) xf= -1:0.1:1; yf= -1:0.1:1; clf() fchamp(derpol,0,xf,yf,1,[-2,-2,2,2],"011")
See also
- champ — plots as arrows a field of 2D vectors
- champ_properties — description of the 2D vector field entity properties
- xarrows — draw a set of arrows in 2D or in 3D.
- Arrowed polyline — description of the Polyline entity properties
| Report an issue | ||
| << errbar | 2d_plot | fec >> |