SUNDIALS Linear Solvers
SUNDIALS direct and iterative, preconditionned linear solvers
Syntax
... = solver( ... , linearSolver = linSol, precType = side, precBand = [mu,ml])
Linear solvers used by SUNDIALS solvers
SUNDIALS solvers may use underlying linear solvers when the selected method needs to solve a linear algebraic system during a method step. This is the case when kinsol is used with the Newton or Picard method or when ODE/DAE solvers use an implicit scheme (arkode uses such a solver with explicit schemes also when a mass matrix is present). When the Jacobian is explicitely provided by the user, either dense, banded or sparse, or implicitely by means of jacBand or jacPattern options, then the corresponding direct solver is used, i.e. Lapack's dense or band solver or KLU sparse solver. The default behavior when a linear solver is needed is to use the dense solver and difference quotients to approximate the Jacobian.
When very large scale problems are considered, matrix-free, scaled, preconditioned, iterative linear solvers are sometimes the only way to go. Although SUNDIALS allows to use this class of solver for ODEs, DAEs and nonlinear equations, for the time being the Scilab module only allows them for ODEs (cvode and arkode solvers) and built-in band preconditioning. The related options are the following:
| linearSolver | The linear solver given as a string:
|
| linSolMaxIters | The maximum number of iterations/Krylov vectors |
| precType | The preconditioning type or side: "RIGHT" (the default), "LEFT", "BOTH" or "NONE". |
| precBand | A vector of two positive integers |
Example
An ODE system is generated from the following 2-species diurnal kinetics advection-diffusion PDE system in 2 space dimensions
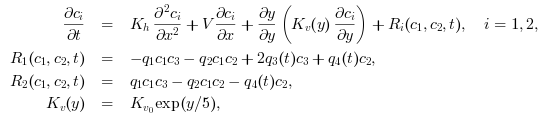
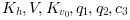 are constants and
are constants and 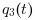 and
and 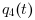 vary diurnaly.
The problem is posed on the square [0,20] x [30, 50] (in km), with homogeneous Neumann boundary conditions,
and for time t in [0,129600] (three days and a half).
The PDE system is treated by central differences on a uniform
100 x 100 mesh, with simple polynomial initial profiles.
vary diurnaly.
The problem is posed on the square [0,20] x [30, 50] (in km), with homogeneous Neumann boundary conditions,
and for time t in [0,129600] (three days and a half).
The PDE system is treated by central differences on a uniform
100 x 100 mesh, with simple polynomial initial profiles.
The problem is solved with cvode, with the BDF/GMRES
method (i.e. using the SUNLinSol_SPGMR linear solver) by passing option linearSolver="GMR"
and a banded preconditioner, generated by difference quotients, using the option precBand. The problem is solved with left and right
preconditioning (this is the default).
In the example below the right-hand side is a compiled C-gateway from the examples of SUNDIALS library. The Scilab interface to cvode allows to
manipulate the state of the discretized PDE as a (2,100,100) 3-dimensional array and the output C of the solver
is a (2,100,100,n) 4-dimensional array where n is the length of the tspan vector. A callback is used to represent the two species
with a pseudo-color plot.
function out=cbFn(t, C, flag, stats) global h1 h2 out = %f; if flag == "init" clf gcf().axes_size = [740 300]; gcf().figure_name = "2-species diurnal kinetics advection-diffusion 2D PDE" gcf().color_map = parulacolormap(128); subplot(1,2,1) title("Species 1") Sgrayplot(x,y,squeeze(C(1,:,:)),zminmax=[0 51146186]) h1 = gce().children; colorbar; subplot(1,2,2) Sgrayplot(x,y,squeeze(C(2,:,:)),zminmax=[0 1.074D+12]) h2 = gce().children; colorbar; title("Species 2") elseif flag == "step" drawlater h1.data(:,3)=C(1,:)'; h2.data(:,3)=C(2,:)'; drawnow gcf().info_message=sprintf("time = %g s",t); end end source = fullfile(SCI,"modules","differential_equations","tests","unit_tests","cvDiurnal_kry_bp.c") SUN_Clink("cvDiurnal_kry_bp_rhs",source,load=%t); PI = 3.1415926535898; TWOHR = 7200.0 // number of seconds in two hours HALFDAY = 4.32e4 // number of seconds in a half day KH = 4.0e-6 // horizontal diffusivity Kh VEL = 0.001 // advection velocity V KV0 = 1.0e-8 // coefficient in Kv(y) RTOL = 1e-5; ATOL = 100*RTOL; MX = 100; // MX and MY values are hard coded in cvDiurnal_kry_bp.c MY = 100; // don't change these values ! XMIN = 0; XMAX = 20; YMIN = 30; YMAX = 50; DX = (XMAX-XMIN)/(MX-1); DY = (YMAX-YMIN)/(MY-1); x = XMIN+(0:MX-1)*DX; y = YMIN+(0:MY-1)*DY; [X,Y] = ndgrid(x,y); q4 = 0; om = PI/HALFDAY; hdco = KH/DX^2; haco = VEL/(2*DX); vdco = KV0/DY^2; user_data = [q4,om,DX,DY,hdco,haco,vdco]; // initial profiles C0 = zeros(2,MX,MY); alph = (0.1*X-1).^2; alph = 1-alph+0.5*alph.^2; bet = (0.1*Y-4).^2; bet = 1-bet+0.5*bet.^2; C0(1,:,:) = 1e6*alph.*bet; C0(2,:,:) = 1e12*alph.*bet; tspan = 0:TWOHR/60:3*HALFDAY; [t,C,info] = cvode(list("cvDiurnal_kry_bp_rhs",user_data), tspan, C0, t0=0, rtol=RTOL, atol=ATOL,... method="BDF", linearSolver="GMR", precBand=[2 2], callback=cbFn);
See also
| Report an issue | ||
| << Options (kinsol) | Options, features and user functions | Options (ODE and DAE solvers) >> |