Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
intg
определённый интеграл
Синтаксис
[v, err] = intg(a, b, f) [v, err] = intg(a, b, f, atol) [v, err] = intg(a, b, f, atol, rtol) [v, err, ierr] = intg(..)
Аргументы
- a, b
- Конечные действительные числа: границы интеграла.
- f
- внешняя функция (функция, список или строка)
- atol
- абсолютная ошибка, требуемая для результата. Значение по умолчанию: 1.d-13.
- rtol
- относительная ошибка, требуемая для результата. Значение по умолчанию: 1.d-8.
- err
- оцененная абсолютная ошибка результата.
- ierr
- error flag number (= 0 if no error occurred).
Описание
intg(a,b,f) вычисляет определённый интеграл функции
f(t) по dt в пределах от
a до b.
Функция f(t) должна быть непрерывной.
Вычисление, как можно ожидать, удовлетворяет следующему условию точности:
abs(I-v)<= max(atol, rtol*abs(I)), где
I -- точное значение интеграла.
f -- внешняя функция:
Если
f-- функция, то её определение должно иметь видy = f(t).Если
f-- список, то этот список должен быть в виде:list(f,x1,x2,...), гдеf-- функция с последовательностью вызоваf(t,x1,x2,...).Если
f-- строка, то она ссылается на имя либо процедуры Fortran либо функции C с заданной последовательностью вызова:в случае Fortran вызывающая последовательность должна быть в виде
double precision function f(x), гдеxтакже является числом двойной точности.В случае C вызывающая последовательность должна быть
double f(double *x).
Используемые функции : Связанные подпрограммы можно найти в директории SCI/modules/differential_equations/src/fortran: dqags.f и dqagse.f из quadpack.
Known Limitation
Like all the integrators, intg is subject to spike missing.
A flat function with a spike will be seen as a fully flat function if the spike is stiff enough.
This cannot be bypassed. It is easy to understand why when we know how the integrator operates.
Indeed, intg uses the 21-point Gauss-Kronrod rule.
Hence, any spike in-between two consecutive integration points will be undetected,
and the function will be considered smooth.
However, a warning message will be issued if the function is considered very smooth. The user will then be suggested to reduce the integration interval, should he think that spikes were missed.
The following graphs illustrate that phenomenon:
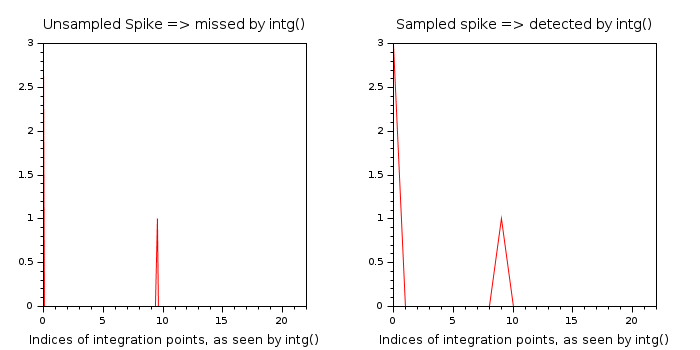
On the left image, the spike lays between the 9th and 10th integration points,
and is not detected. intg considers the function flat.
On the right, the spike is large enough to be covered by the integration points.
 | When we want to display the computed solution even if the solver has encountered an error,
we should add the third output argument ierr. Then errors become
simple warnings. This is mostly used in the case of rounding errors. |
Примеры
// Функция, написанная на языке Scilab function y=f(x), y = x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)), endfunction exact = -2.5432596188; I = intg(0, 2*%pi, f) abs(exact - I) // Функция с аргументом, написанном на языке Scilab function y=f1(x, w), y=x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)), endfunction I = intg(0, 2*%pi, list(f1,30)) abs(exact - I) // Функция, написанная на Fortran (требуется компилятор Fortran) // определение функции Fortran cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F, 'ffun.f') // компилируем функцию l = ilib_for_link('ffun', 'ffun.f', [], 'f'); // добавляем функцию в рабочее окружение link(l, 'ffun', 'f') // интегрируем функцию I = intg(0, 2*%pi, 'ffun') abs(exact - I) // Функция, написанная на C (требуется компилятор C) // определение C-функции C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C, 'cfun.c') // компилируем функцию l = ilib_for_link('cfun', 'cfun.c', [], 'c'); // добавляем функцию в рабочее окружение link(l, 'cfun', 'c') // интегрируем функцию I = intg(0, 2*%pi, 'cfun') abs(exact - I)
Смотрите также
История
| Версия | Описание |
| 6.0.2 | The default value atol of the absolute tolerance is increased from 1O-14 to 1O-13. |
| Report an issue | ||
| << integrate | Дифференциальное счисление, интегрирование | intl >> |