Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
intg
integral definida
Seqüência de Chamamento
[v, err] = intg(a, b, f) [v, err] = intg(a, b, f, atol) [v, err] = intg(a, b, f, atol, rtol) [v, err, ierr] = intg(..)
Parâmetros
- a, b
- Números reais finitos: limites da integral.
- f
- função externa (função, lista ou string)
- atol
- Número real: erro absoluto requerido no resultado. Valor padrão: 1.d-13.
- rtol
- Número real: erro relativo requerido no resultado. Valor padrão: 1.d-8.
- err
- erro absoluto estimado no resultado
- ierr
- error flag number (= 0 if no error occurred).
Descrição
intg(a,b,f) avalia a integral definida de
a a b de f(t)dt.
A função f(t) deve ser contínua.
Espera-se que a avaliação satisfaça à seguinte precisão:
abs(I-v)<= max(atol,er*abs(I)) onde I é o valor exato
da integral.
f é uma função externa :
Se f é uma função, sua definição deve ser como
segue: y = f(t)
Se f é uma lista, a lista deve ser como segue:
list(f,x1,x2,...) onde f é uma
função com seqüência de chamamento
f(t,x1,x2,...).
Se f é um string, ele se refere ao nome de uma
função FORTRAN ou procedure C com dada seqüência de chamamento:
No caso FORTRAN, a seqüência de chamamento deve ser
double precision function f(x)
onde x tabém é um número de dupla precisão.
No caso C, a seqüência de chamamento é double f(double *x).
Funções Utilizadas : As rotinas associadas (dqags.f e dqagse.f de quadpack) podem ser encontradas no diretório SCI/modules/differential_equations/src/fortran.
Known Limitation
Like all the integrators, intg is subject to spike missing.
A flat function with a spike will be seen as a fully flat function if the spike is stiff enough.
This cannot be bypassed. It is easy to understand why when we know how the integrator operates.
Indeed, intg uses the 21-point Gauss-Kronrod rule.
Hence, any spike in-between two consecutive integration points will be undetected,
and the function will be considered smooth.
However, a warning message will be issued if the function is considered very smooth. The user will then be suggested to reduce the integration interval, should he think that spikes were missed.
The following graphs illustrate that phenomenon:
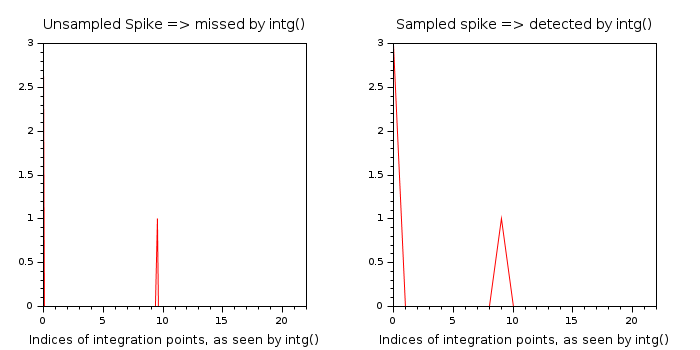
On the left image, the spike lays between the 9th and 10th integration points,
and is not detected. intg considers the function flat.
On the right, the spike is large enough to be covered by the integration points.
 | When we want to display the computed solution even if the solver has encountered an error,
we should add the third output argument ierr. Then errors become
simple warnings. This is mostly used in the case of rounding errors. |
Exemplos
// caso de função Scilab function y=f(x), y = x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)), endfunction exact = -2.5432596188; I = intg(0, 2*%pi, f) abs(exact - I) // caso de função Scilab com parâmetros function y=f1(x, w), y = x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)), endfunction I = intg(0, 2*%pi, list(f1,30)) abs(exact - I) // caso de código FORTRAN (compilador FORTRAN requerido) // escreve o código FORTRAN cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F, 'ffun.f') // compile o código FORTRAN l = ilib_for_link('ffun', 'ffun.f', [], 'f'); // linking incremental link(l, 'ffun', 'f') // integrando a função I = intg(0, 2*%pi, 'ffun') abs(exact - I) // caso de código C (compilador C requerido) // escreva o código C C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C, 'cfun.c') // compile o código C l = ilib_for_link('cfun', 'cfun.c', [], 'c'); // linking incremental link(l, 'cfun', 'c') //integrando a função I = intg(0, 2*%pi, 'cfun') abs(exact - I)
Ver Também
Histórico
| Versão | Descrição |
| 6.0.2 | The default value atol of the absolute tolerance is increased from 10-14 to 10-13. |
| Report an issue | ||
| << integrate | Equações Diferenciais | intl >> |