dae

Аргументы

initial

вектор-столбец. Он может быть равен x0 или [x0;xdot0], где x0 - это значение состояния в начальный момент времени t0, а xdot0 - значение производной исходного состояния или его оценка (см. ниже).

t0

вещественное число, исходный момент времени.

t

Вещественный скаляр или вектор. Указывает моменты времени для которых нужно найти решение. Заметьте, что вы можете получить решение в каждой точке шага ДАУ с помощью установки %DAEOPTIONS(2)=1 .

rtol

вещественный скаляр или вектор-столбец того же размера, что и x0, допуск относительной ошибки. Если rtol является вектором, то допуски определяются для каждой составляющей состояния.

atol

вещественный скаляр или вектор-столбец того же размера, что и x0, допуск абсолютной ошибки. Если atol является вектором, то допуски определяются для каждой составляющей состояния.

res

внешняя функция, которая вычисляет значение g(t,y,ydot). Она может быть:

функцией Scilab'а

В этом случае последовательность вызова должна быть [r,ires]=res(t,x,xdot), а res должна возвращать остаток r=g(t,x,xdot) и флаг ошибки ires.

ires = 0, если res смогла вычислить r;

ires = -1, если остаток для g(t,x,xdot) локально не определён;

ires =-2, если параметры находятся вне допустимого диапазона.

списком

Эта форма внешней функции используется для передачи параметров в функцию. Она может иметь следующий вид:

list(res,p1,p2,...)

где последовательность вызова функции res теперь

r=res(t,y,ydot,p1,p2,...)

Функция res по-прежнему возвращает значение остатка в виде функции от (t,x,xdot,x1,x2,...), а p1, p2,... являются параметрами функции.

символьной строкой

она должна ссылаться на имя подпрограммы на языке C или fortran, в предположении, что <r_name> является заданным именем.

• Последовательность вызова Fortran должна быть

  <r_name>(t, x, xdot, res, ires, rpar, ipar)

  t, x(*), xdot(*), res(*), rpar(*) имеют удвоенную точность;

  ires, ipar(*) являются целочисленными.

• Последовательность вызова C должна быть

  C2F(<r_name>)(double *t, double *x, double *xdot, double *res, integer *ires, double *rpar, integer *ipar) ,

где

• t - текущее значение времени;

• x - массив состояния;

• xdot - массив производных состояния;

• res - массив остатков;

• ires - индикатор выполнения;

• rpar - массив целочисленных значений параметров с плавающей запятой, которые нужны, но не могут быть установлены с помощью функции dae.

• ipar - массив целочисленных значений параметров с плавающей запятой, которые нужны, но не могут быть установлены с помощью функции dae.

jac

Внешняя функция вычисляет значение dg/dx+cj*dg/dxdot для заданного значения параметра cj. Она может быть

функцией Scilab'а

В этом случае последовательность вызова должна быть r=jac(t,x,xdot,cj), а jac должна возвращать r=dg(t,x,xdot)/dy+cj*dg(t,x,xdot)/dxdot, где cj - вещественный скаляр.

списком

Эта форма внешней функции используется для передачи параметров в функцию. Она может иметь следующий вид:

list(jac,p1,p2,...)

где последовательность вызова функции jac теперь

r=jac(t,x,xdot,p1,p2,...)

Функция jac по-прежнему возвращает dg/dx+cj*dg/dxdot как функцию от (t, x, xdot, cj, p1, p2,...).

символьной строкой

она должна ссылаться на имя подпрограммы на языке C или fortran, в предположении, что <j_name> является заданным именем.

• Последовательность вызова Fortran должна быть

  <j_name>(t, x, xdot, r, cj, ires, rpar, ipar)

  t, x(*), xdot(*), r(*), ci, rpar(*) имеют удвоенную точность;

  ires, ipar(*) являются целочисленными.

• Последовательность вызова C должна быть

  C2F(<j_name>)(double *t, double *x, double *xdot, double *r, double *cj, integer *ires, double *rpar, integer *ipar) ,

где t, x, xdot, ires, rpar, ipar имеют аналогичное определение, что и выше, r - массив результатов

surface

Внешняя функция вычисляет значение вектор-столбца surface(t,x) с количеством элементов ng. Каждый элемент определяет поверхность.

функцией Scilab'а

В этом случае последовательность вызова должна быть r=surface(t,x). Эта функция должна вернуть вектор с ng элементами.

списком

Эта форма внешней функции используется для передачи параметров в функцию. Она может иметь следующий вид:

list(surface,p1,p2,...)

где последовательность вызова функции surface теперь имеет вид:

r=surface(t,x,p1,p2,...)

символьной строкой

она должна ссылаться на имя подпрограммы на языке C или fortran, в предположении, что <s_name> является заданным именем.

• Последовательность вызова Fortran должна быть

  <j_name>(t, x, xdot, r, cj, ires, rpar, ipar)

  t, x(*), xdot(*), r(*), ci, rpar(*) имеют удвоенную точность;

  ires, ipar(*) являются целочисленными.

• Последовательность вызова C должна быть

  C2F(<j_name>)(double *t, double *x, double *xdot, double *r, double *cj, integer *ires, double *rpar, integer *ipar) ,

где t, x, xdot, ires, rpar, ipar имеют аналогичное определение, что и выше, ng - количество поверхностей, nx - размерность состояния и r - массив результатов.

rd

вектор с двумя элементами [times num], где times - значение момента времени пересечения поверхности, num - число пересечённых поверхностей

hd

вещественный вектор, в качестве аргумента на выходе он хранит контекст dae. Он может быть использован в качестве входного аргумента для возобновления интегрирования (горячий перезапуск).

y

вещественная матрица. Если %DAEOPTIONS(2)=1 ,то каждый столбец является вектором вида [t;x(t);xdot(t)], где t - индекс времени для которого вычислено решение. В противном случае y - вектор вида [x(t);xdot(t)].

Описание

Функция dae является шлюзом, построенным над функциями dassl и dasrt, разработанными для явного интегрирования дифференциальных уравнений.

            g(t,x,xdot) = 0
            x(t0) = x0  and   xdot(t0) = xdot0

Если xdot0 не указан в исходном аргументе, то функция dae пытается вычислить его решая уравнение g(t,x0,xdot0)=0/

Если xdot0 указан в исходном аргументе, то он может быть либо совместимой производной (compatible derivative), удовлетворяющей условию g(t,x0,xdot0)=0, либо приближённым значением. В последнем случае %DAEOPTIONS(7) должен быть установлен в 1.

Конкретные примеры использования внешних функций, написанных на языке Scilab и C, представлены в modules/differential_equations/tests/unit_tests/dassldasrt.tst

Примеры

// Пример с кодом Scilab
// -------------------------------------------
function [r, ires]=chemres(t, y, yd)
    r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1);
    r(2) =  0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2);
    r(3) =       y(1) +     y(2)      + y(3)-1;
    ires =  0;
endfunction

function pd=chemjac(x, y, yd, cj)
    pd = [-0.04-cj , 1d4*y(3)               , 1d4*y(2);
           0.04    ,-1d4*y(3)-2*3d7*y(2)-cj ,-1d4*y(2);
           1       , 1                      , 1       ]
endfunction

x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400, 4000, 40000, 4d5, 4d6, 4d7, 4d8, 4d9, 4d10];

y = dae([x0, xd0], 0, t, chemres); // возвращает запрошенные моменты времени наблюдения

%DAEOPTIONS = list([], 1, [], [], [], 0, 0); // просит вернуть сетку точек dae
y = dae([x0, xd0], 0, 4d10, chemres); // без якобиана
y = dae([x0, xd0], 0, 4d10, chemres, chemjac); // с якобианом

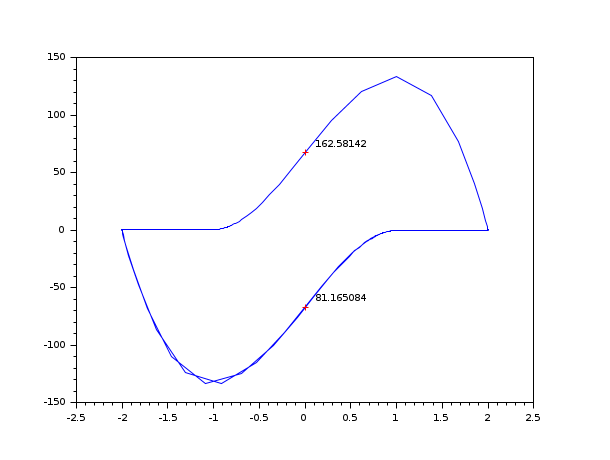
// пример с кодом C (необходим C-компилятор)
// -----------------------------------------
bOK = haveacompiler();
if bOK <> %t
    [btn] = messagebox(["Для этого примера Вам необходим C-компилятор.";"Выполнение этого примера отменено."], "Проблема с программным обеспечением", 'info');
    return
end

//-1- создать C-код в TMPDIR - Уравнение Вандерпола, неявная форма
code = ['#include <math.h>'
      'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)'
      '{res[0] = yd[0] - y[1];'
      ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}'
      ' '
      'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)'
      '{pd[0] = *cj - 0.0;'
      ' pd[1] =     - (-200.0*y[0]*y[1] - 1.0);'
      ' pd[2] =     - 1.0;'
      ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}'
      ' '
      'void gr22(int *neq, double *t, double *y, int *ng, double *groot, double *rpar, int *ipar)'
      '{ groot[0] = y[0];}']
previous_dir = pwd();
cd TMPDIR;
mputl(code, 't22.c')

//-2- скомпилировать и загрузить его
ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce');
exec('t22loader.sce')

//-3- запустить
rtol = [1.d-6; 1.d-6];
atol = [1.d-6; 1.d-4];
t0 = 0; t = [20:20:200];
y0 = [2; 0]; y0d = [0; -2];
ng = 1;

//простое моделирование
t = 0:0.003:300;
yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22');
clf(); plot(yy(1, :), yy(2, :))
// Найти первую точку, где yy(1) = 0
[yy, nn, hotd] = dae("root", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22');
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));

// горячий перезапуск для следующей точки
t01 = nn(1);
[pp, qq] = size(yy);
y01 = yy(2:3, qq); y0d1 = yy(3:4, qq);
[yy, nn, hotd] = dae("root", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', hotd);
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));
cd(previous_dir);

Смотрите также

• ode — программа решения обыкновенных дифференциальных уравнений
• daeoptions — установка опций для dae (программа решения дифференциальных алгоритмических уравнений)
• dassl — дифференциальное алгебраическое уравнение
• impl — дифференциальное алгебраическое уравнение
• call — Fortran or C user routines call
• link — dynamic linker
• external — объект Scilab'а, внешняя функция или подпрограмма