Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
dae
微分代数方程式ソルバ
呼び出し手順
y = dae(initial, t0, t, res) [y [,hd]] = dae(initial, t0, t [[,rtol], atol], res [,jac] [,hd]) [y, rd] = dae("root", initial, t0, t, res, ng, surface) [y, rd [,hd]] = dae("root", initial, t0, t [[,rtol], atol], res [,jac], ng, surface [,hd]) [y, rd] = dae("root2", initial, t0, t, res, ng, surface) [y, rd [,hd]] = dae("root2", initial, t0, t [[,rtol], atol], res [,jac], ng, surface [, psol, pjac] [, hd])
引数
- initial
列ベクトル.
x0または[x0;xdot0]とします. ただし,x0は 初期時刻t0における状態量の値,ydot0は状態量の微分の初期値 またはその推定値(下記参照)です.- t0
実数, 初期時刻.
- t
実数のスカラーまたはベクトル. 解を計算する時刻を指定します.
%DAEOPTIONS(2)=1と設定することにより DAEの各ステップで解が得られることに注意してください.- atol
実数のスカラーまたは
x0と同じ大きさの 列ベクトル. 解の絶対許容誤差.atolがベクトルの場合, 状態量の各要素毎に許容誤差が指定されます.- rtol
実数のスカラーまたは
x0と同じ大きさの 列ベクトル. 解の相対許容誤差.rtolがベクトルの場合, 状態量の各要素毎に許容誤差が指定されます.- res
外部ルーチン.
g(t,y,ydot)の値を計算します. 以下のようになります- Scilab関数
この場合, その呼出し手順を
[r,ires]=res(t,x,xdot)とする 必要があり,resは 残差r=g(t,x,xdot)とエラーフラグiresを返す必要があります.resがrの計算に 成功した場合にはires = 0,(t,x,xdot)のローカルな残差が定義されない 場合には=-1, パラメータが許容範囲外の場合は=-2となります.- リスト
外部ルーチンのこの形式は 関数にパラメータを指定する際に使用されます. 以下のような形式とします:
list(res,p1,p2,...)
ただし,ここで関数
resの呼び出し手順は以下のようになりますr = res(t,y,ydot,p1,p2,...)
この場合も
resは(t,x,xdot,x1,x2,...)の関数として残差の値を返し, p1,p2,... は関数のパラメータです.- 文字列
CまたはFortranルーチンの名前を指します. <r_name> が指定した名前であると仮定します.
Fortranの呼出し手順は以下のようにします
<r_name>(t,x,xdot,res,ires,rpar,ipar)double precision t,x(*),xdot(*),res(*),rpar(*)integer ires,ipar(*)Cの呼出し手順は以下のようにします
C2F(<r_name>)(double *t, double *x, double *xdot, double *res, integer *ires, double *rpar, integer *ipar)
ただし,
tはカレントの時刻xは状態量の配列xdotは状態量の微分の配列res は残差の配列
iresは実行インジケータrparは浮動小数点数の パラメータ値の配列で, 必要ですがdae関数により 設定できないものiparは整数の パラメータ値の配列で, 必要ですがdae関数により 設定できないもの
- jac
外部ルーチン. 指定したパラメータの値
cjを用いてdg/dx+cj*dg/dxdotの値を計算します. 以下のようになります- Scilab関数
呼出し手順を
r=jac(t,x,xdot,cj)とする 必要があり,jac関数はr=dg(t,x,xdot)/dy+cj*dg(t,x,xdot)/dxdotを返す必要があります. ただし,cjは実数スカラーです.- リスト
外部ルーチンのこの形式は 関数にパラメータを指定する際に使用されます. 以下のような形式とします:
list(jac,p1,p2,...)
ただしこの場合の関数
jacの呼び出し手順は 以下となりますr = jac(t,x,xdot,p1,p2,...)
この場合でも
jacは,(t,x,xdot,cj,p1,p2,...)の関数としてdg/dx+cj*dg/dxdotを返します.- 文字列
CまたはFortranルーチンの名前を指します. <j_name> が指定した名前であると仮定します.
Fortranの呼出し手順は以下のようにします
<j_name>(t, x, xdot, r, cj, ires, rpar, ipar)double precision t, x(*), xdot(*), r(*), ci, rpar(*)integer ires, ipar(*)Cの呼出し手順は以下のようにします
C2F(<j_name>)(double *t, double *x, double *xdot, double *r, double *cj,
integer *ires, double *rpar, integer *ipar)
ただし
t, x, xdot, ires, rpar, ipar は上記と似た定義を有し, r は配列の結果です.
- surface
外部ルーチン.
ng個の要素を有する列ベクトルsurface(t,x)の値を計算します. 各要素は面(surface)を定義します.- Scilab関数
その呼び出し手順は
r=surface(t,x)とする 必要があり,この関数はng個の要素を有する ベクトルを返す必要があります.- リスト
外部ルーチンのこの形式は 関数にパラメータを指定する際に使用されます. 以下のような形式とします:
list(surface,p1,p2,...)
ただしこの場合の関数
surfaceの呼び出し手順は 以下となりますr = surface(t,x,p1,p2,...)
- 文字列
CまたはFortranルーチンの名前を指します. <s_name> が指定した名前であると仮定します,
Fortranの呼出し手順は以下のようにします
<r_name>(nx, t, x, ng, r, rpar, ipar)double precision t, x(*), r(*), rpar(*)integer nx, ng,ipar(*)Cの呼出し手順は以下のようにします
C2F(<r_name>)(double *t, double *x, double *xdot, double *r, double *cj,
integer *ires, double *rpar, integer *ipar)
ただし,
t, x, rpar, ipar は 上記と同じ定義を有し,ngは surfacesの数,nxは状態量の次元, r は結果の配列です.
- rd
2個のエントリ
[times num]を有するベクトル.timesは面が交差した時刻の値,numは交差した面の数です- pjac
外部 (関数, リストまたは文字列). daskr参照.
- psol
外部 (関数, リストまたは文字列). daskr参照.
- hd
実数のベクトル,
daeコンテキストを保持する出力. (ホットスタートで)積分を再開するための入力引数として使用可能です.- y
実数の行列.
%DAEOPTIONS(2)=1の場合, 各列 はベクトル[t;x(t);xdot(t)]です. ただし,tは解が計算された時刻です. それ以外の場合,yはベクトル[x(t);xdot(t)]です.
説明
dae 関数は,
陰的な微分方程式積分用に設計された
dassl および dasrt
関数の上位に構築されたゲートウエイです.
オプション "root" は
dasrt ルーチンをコールし,
"root2" は daskrをコールします.
g(t,x,xdot) = 0 x(t0) = x0 および xdot(t0)=xdot0
initial引数にxdot0 が指定されない場合,
dae関数は g(t,x0,xdot0)=0
を解くことによりこれを計算しようとします.
xdot0 が initial引数で指定された場合,
g(t,x0,xdot0)=0を満たす互換性がある微係数または近似値の
どちらかとなります.
後者の場合,
%DAEOPTIONS(7)
を 1 に設定する必要があります.
Scilab および C でコーディングされた外部ルーチンを使用する詳細な例については,
modules/differential_equations/tests/unit_tests/dassldasrt.tst
および
modules/differential_equations/tests/unit_tests/daskr.tst
で提供されています.
例
例 #1: dassl (求解なし)
// Scilabコードを使用する例 function [r, ires]=chemres(t, y, yd) r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1); r(2) = 0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2); r(3) = y(1) + y(2) + y(3)-1; ires = 0; endfunction function pd=chemjac(x, y, yd, cj) pd=[-0.04-cj , 1d4*y(3) , 1d4*y(2); 0.04 ,-1d4*y(3)-2*3d7*y(2)-cj ,-1d4*y(2); 1 , 1 , 1 ] endfunction x0 = [1; 0; 0]; xd0 = [-0.04; 0.04; 0]; t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400, 4000, 40000, 4d5, 4d6, 4d7, 4d8, 4d9, 4d10]; y = dae([x0,xd0],0,t,chemres);// 指定した観測時刻での点を返す %DAEOPTIONS = list([],1,[],[],[],0,0); // dae メッシュ点を返すかどうかを確認 y = dae([x0,xd0],0,4d10,chemres); // ヤコビアン指定なし y = dae([x0,xd0],0,4d10,chemres,chemjac); // ヤコビアン指定あり
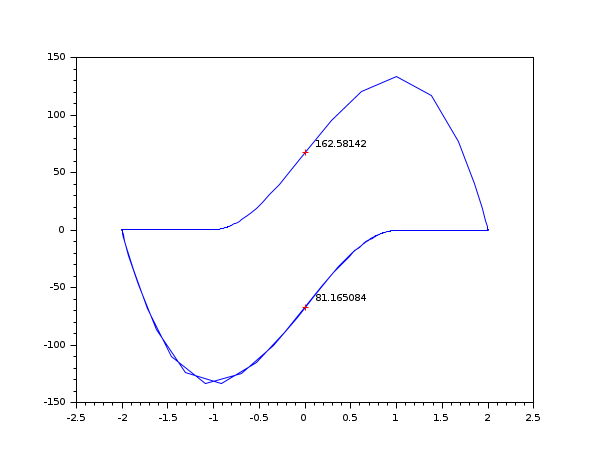
例 #2: dasrt ("root")
// C コードの例 (Cコンパイラが必要) -------------------------------------------------- bOK = haveacompiler(); if bOK <> %t [btn] = messagebox(["You need a C compiler for this example."; "Execution of this example is canceled."], "Software problem", 'info'); return end //-1- Cコードを TMPDIR に作成 - Vanderpol 方程式, 陰形式 code=['#include <math.h>' 'void res22(double *t,double *y,double *yd,double *res,int *ires,double *rpar,int *ipar)' '{res[0] = yd[0] - y[1];' ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}' ' ' 'void jac22(double *t,double *y,double *yd,double *pd,double *cj,double *rpar,int *ipar)' '{pd[0]=*cj - 0.0;' ' pd[1]= - (-200.0*y[0]*y[1] - 1.0);' ' pd[2]= - 1.0;' ' pd[3]=*cj - (100.0*(1.0 - y[0]*y[0]));}' ' ' 'void gr22(int *neq, double *t, double *y, int *ng, double *groot, double *rpar, int *ipar)' '{ groot[0] = y[0];}'] mputl(code,TMPDIR+'/t22.c') //-2- コンパイルの後,ロード ilib_for_link(['res22' 'jac22' 'gr22'],'t22.c',[],'c',[],TMPDIR+'/t22loader.sce'); exec(TMPDIR+'/t22loader.sce') //-3- 実行 rtol = [1.d-6;1.d-6];atol=[1.d-6;1.d-4]; t0 = 0; y0 = [2;0]; y0d = [0;-2]; t = [20:20:200]; ng = 1; //簡単なシミュレーション t = 0:0.003:300; yy = dae([y0,y0d],t0,t,atol,rtol,'res22','jac22'); clf(); plot(yy(1,:),yy(2,:)) //find first point where yy(1)=0 [yy,nn,hotd] = dae("root",[y0,y0d],t0,300,atol,rtol,'res22','jac22',ng,'gr22'); plot(yy(1,1),yy(2,1),'r+') xstring(yy(1,1)+0.1,yy(2,1),string(nn(1))) //次の点までホットリスタート t01 = nn(1); [pp,qq] = size(yy); y01 = yy(2:3,qq); y0d1 = yy(3:4,qq); [yy,nn,hotd] = dae("root",[y01,y0d1],t01,300,atol,rtol,'res22','jac22',ng,'gr22',hotd); plot(yy(1,1),yy(2,1),'r+') xstring(yy(1,1)+0.1,yy(2,1),string(nn(1))); cd(previous_dir);
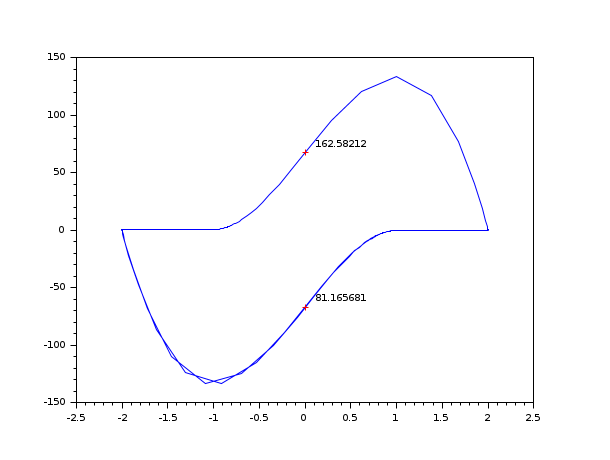
例 #3: daskr ("root2"), デフォルトの 'psol' および 'pjac' ルーチンを使用
// Example with C code (C compiler needed) //-------------------------------------------------- bOK = haveacompiler(); if bOK <> %t [btn] = messagebox(["You need a C compiler for this example."; "Execution of this example is canceled."], "Software problem", 'info'); return end //-1- Create the C codes in TMPDIR - Vanderpol equation, implicit form code = ['#include <math.h>' 'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)' '{res[0] = yd[0] - y[1];' ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}' ' ' 'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)' '{pd[0] = *cj - 0.0;' ' pd[1] = - (-200.0*y[0]*y[1] - 1.0);' ' pd[2] = - 1.0;' ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}' ' ' 'void gr22(int *neq, double *t, double *y, int *ng, double *groot, double *rpar, int *ipar)' '{ groot[0] = y[0];}'] previous_dir = pwd(); cd TMPDIR; mputl(code, 't22.c') //-2- Compile and load them ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce'); exec('t22loader.sce') //-3- Run rtol = [1.d-6; 1.d-6]; atol = [1.d-6; 1.d-4]; t0 = 0; t = [20:20:200]; y0 = [2; 0]; y0d = [0; -2]; ng = 1; // Simple simulation t = 0:0.003:300; yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22'); clf(); plot(yy(1, :), yy(2, :)) // Find first point where yy(1) = 0 %DAEOPTIONS = list([] , 0, [], [], [], 0, [], 1, [], 0, 1, [], [], 1); [yy, nn, hotd] = dae("root2", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1'); plot(yy(1, 1), yy(2, 1), 'r+') xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1))); // Hot restart for next point t01 = nn(1); [pp, qq] = size(yy); y01 = yy(2:3, qq); y0d1 = yy(3:4, qq); [yy, nn, hotd] = dae("root2", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1', hotd); plot(yy(1, 1), yy(2, 1), 'r+') xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1))); cd(previous_dir);
参照
| Report an issue | ||
| << bvode | Differential Equations, Integration | daeoptions >> |