Scilab 6.1.0
- Scilab Help
- Signal Processing
- Filters
- How to design an elliptic filter
- analpf
- buttmag
- casc
- cheb1mag
- cheb2mag
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- filt_sinc
- filter
- find_freq
- frmag
- fsfirlin
- group
- hilbert
- iir
- iirgroup
- iirlp
- kalm
- lev
- levin
- lindquist
- remez
- remezb
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wfir_gui
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ell1mag
magnitude of elliptic filter
Syntax
[v]=ell1mag(eps,m1,z)
Arguments
- eps
passband ripple=
1/(1+eps^2)- m1
stopband ripple=
1/(1+(eps^2)/m1)- z
sample vector of values in the complex plane
- v
elliptic filter values at sample points
Description
Function used for squared magnitude of an elliptic filter.
Usually m1=eps*eps/(a*a-1). Returns
v=real(ones(z)./(ones(z)+eps*eps*s.*s)) for s=ellipj(z,m1).
Examples
deff('[alpha,BeTa]=alpha_beta(n,m,m1)',... 'if 2*int(n/2)==n then, BeTa=K1; else, BeTa=0;end;'+... 'alpha=%k(1-m1)/%k(1-m);') epsilon=0.1;A=10; //ripple parameters m1=(epsilon*epsilon)/(A*A-1);n=5;omegac=6; m=find_freq(epsilon,A,n);omegar = omegac/sqrt(m) %k(1-m1)*%k(m)/(%k(m1)*%k(1-m))-n //Check... [alpha,Beta]=alpha_beta(n,m,m1) alpha*delip(1,sqrt(m))-n*%k(m1) //Check samples=0:0.01:20; //Now we map the positive real axis into the contour... z=alpha*delip(samples/omegac,sqrt(m))+Beta*ones(samples); plot(samples,ell1mag(epsilon,m1,z))
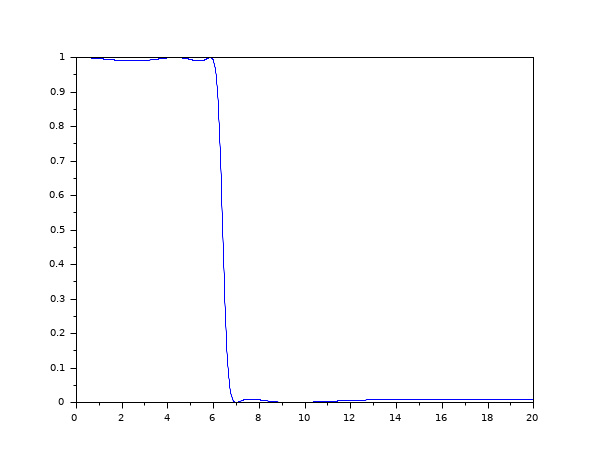
See also
- buttmag — Power transmission of a Butterworth filter
| Report an issue | ||
| << cheb2mag | Filters | eqfir >> |