Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
unwrap
Y(x)輪郭またはZ(x,y)面をアンラップする. Y(x)輪郭を展開する
呼び出し手順
unwrap() // 例を実行 [U, breakPoints] = unwrap(Y) [U, breakPoints] = unwrap(Y, z_jump) [U, cuspPoints] = unwrap(Y, "unfold") U = unwrap(Z) U = unwrap(Z, z_jump) U = unwrap(Z, z_jump, dir)
引数
- Y
実数ベクトル: アンラップまたは展開する外形. 暗黙の座標軸Xが等間隔であることを仮定します.
- Z
実数の行列: アンラップする面. 暗黙の座標軸 (X,Y) は直交軸で等間隔(間隔はXとYで異なることが可能)と仮定されます.
- z_jump
アンラップモードで使用される正のスカラー実数: アンラップを実行する.不連続点で適用されるジャンプ高さ. 絶対値のみが考慮されます. 実際に適用されるジャンプは各不連続点の 両端をつなぐ傾きの符号を有します. デフォルト値は,
z_jump = 2*%piです. 特別な値z_jump = 0は, 各不連続点の周辺の平均的な傾きに 等しいジャンプを適用し, 外形または面全体に連続的な傾きを回復します.- dir
"c" | "r" | "" (デフォルト): アンラップを行う方向. "c" は列方向にアンラップ, "r" は行方向にアンラップ, "" は両方向にアンラップします.
- "unfold"
指定した曲線が折り畳まれている場合,アンラップではなく,展開します.
- U
外形または面をアンラップ, または外形を展開します.
UはYまたはZと同じ大きさとなります.- breakPoints, cuspPoints
Yの点の添字のベクトル. ただし,ラップ及び折りたたみが検出され,処理されています.
説明
アンラップ処理
unwrap() は,例えば
Y = modulo(X,w) または
Y = atan(tan(X))のような
周期的で単調な関数により外形またはラップされた面を
処理する際に有用です.
この関数は,これらの関数の逆関数のように,
制限された
w または [-%pi/2, %pi/2]
の範囲ではなく,全領域で入力 X を復元する
目的で使用されます.
ラップされた外形のブレークポイントは, 点の近傍の両端の傾きがほぼ同じだが(絶対値が)非常に小さく, 考慮される点における傾きとは逆となる点として検出されます: この点において, 近傍の傾きを分断し, 逆となるジャンプがあります.
この検出方法はラップするものを特定のレベルで考慮する ことを避けます. これにより,後で定数(またはトレンドすらも)を追加された ラップされた外形を処理できるようになります.
アンラップ処理は,全ての検出されたジャンプを減らし,
(元が連続だったとすると)一部を連続した傾きに回復します.
この処理は,各点における外形のその他の面に関する全側面への
Y-シフト適用により行われます.
Yシフトは,ユーザにより指定されるため,
全てのブレークポイントで同じとなる可能性があります.
ユーザがYシフトにヌルを指定した場合,
unwrap() は,
各ブレークポイントに依存して近傍の平均的傾きに
等しいジャンプを適用します.
 | アンラップされた外形は常に定義されますが,
一定ではありません. |
dir が使用されない限り,
unwrap() は面の最初の列を
アンラップします.
これらのデータの各点がその点から始まる各線をアンラップする
基準レベルとして使用されます.
展開処理
キーワード"unfold" が使用され,
面ではなく外形が指定された場合,
外形はラップされているのではなく折り畳まれていると
仮定されます.
折りたたみ点 -- または "尖点" -- において, 外形は連続ですが,その傾きは不連続になります: 傾きは絶対値がその両側の点でほぼ等しくなりますが, 両側で逆方向になります.
折りたたみは例えばY= acos(cos(X))
のように非単調周期関数およびその逆関数が
外形Xに適用された場合に発生します.
YからXを回復するのはラップされた場合と比べてはるかに困難です.
実際,
外形が準水平切片の一つの上に接線方向に折り畳まれた場合のように,
あいまいな状況が存在する可能性があります.
尖点を検出した場合, a) そこから始まる外形の片側が逆方向(反対)となり, かつ, b) 外形と傾きの連続性が保持され,考慮する点 (局所的な傾きに基づく小さなジャンプを付加する必要が あるかもしれません)で回復されます.
 | 入力される外形の左端の傾きが最初の基準として
使用されます.展開された外形は元の本当の外形に
対して上下逆となる可能性があります.
加えて,アンラップする場合,定義はされますが
一定となります. |
既知の制限: 現在, 折り畳まれている面は処理できません.
例
1次元の外形をアンラップまたは展開:
// 1次元の例 // ----------- f = scf(); f.figure_size = [800 1000]; f.figure_position(2) = 0; f.figure_name = "unwrap() & ""unfold""" + _(": 1-D examples "); ax = gda(); ax.y_label.font_size=2; drawlater() // 元の1次元の外形 t = linspace(-4,4.2,800); alpha = t.^2 + t -1; subplot(5,2,1) titlepage("unwrap(): unwrap | unfold") subplot(5,2,2) plot(t,alpha) t2 = "$\text{Original profile: } \alpha=t^2+t-1$"; ax = gca(); ax.tight_limits = "on"; yT = max(alpha) - strange(alpha)*0.1; xstring(0,yT,t2) e = gce(); e.text_box_mode = "centered"; e.font_size = 2; // 複数の例をループ for i=1:4 subplot(5,2,2*i+1) if i==1 then // atan(tan())でアンラップ ralpha = atan(tan(alpha)); // 回復したalpha [pi] ylabel("$atan(tan(\alpha))$") [u, K] = unwrap(ralpha, %pi); // arctan t2 = "$\text{unwrap(Y, \%pi)}$"; elseif i==2 // modulo() + Y-シフトでアンラップ c = (rand(1,1)-0.5)*4; ralpha = pmodulo(alpha, 5) + c; ylabel("$modulo(\alpha,\ 5)"+msprintf("%+5.2f",c)+"$") [u, K] = unwrap(ralpha, 0); t2 = "$\text{unwrap(Y, 0)}$"; elseif i==3 // asin(sin()) + Y-シフトで展開 ralpha = 1+asin(sin(alpha)); // 回復したalpha [2.pi] ylabel("$1+asin(sin(\alpha))$") [u, K] = unwrap(ralpha, "unfold"); t2 = "$\text{unwrap(Y,""unfold"")}$"; else // acos(cos()) + トレンド で折りたたみ ralpha = 1+alpha/10+acos(cos(alpha)); // 回復したalpha [2.pi] ylabel("$1+\frac{\alpha}{10}+acos(cos(\alpha))$") [u, K] = unwrap(ralpha, "unfold"); t2 = "$\text{unwrap(Y,""unfold"")}$"; end // 処理する外形をプロット plot(t, ralpha) // 曲線の不連続点または尖点に星印を付けます: if K~=[] then plot(t(K), ralpha(K),"*") end // 処理(展開またはアンラップ)した外形をプロットします: subplot(5,2,2*i+2) plot(t,u) ax = gca(); ax.tight_limits = "on"; // Adding a legend: yT = max(u) - strange(u)*0.2; xstring(0,yT,t2) e = gce(); e.text_box_mode = "centered"; e.font_size = 2; end sda(); drawnow()
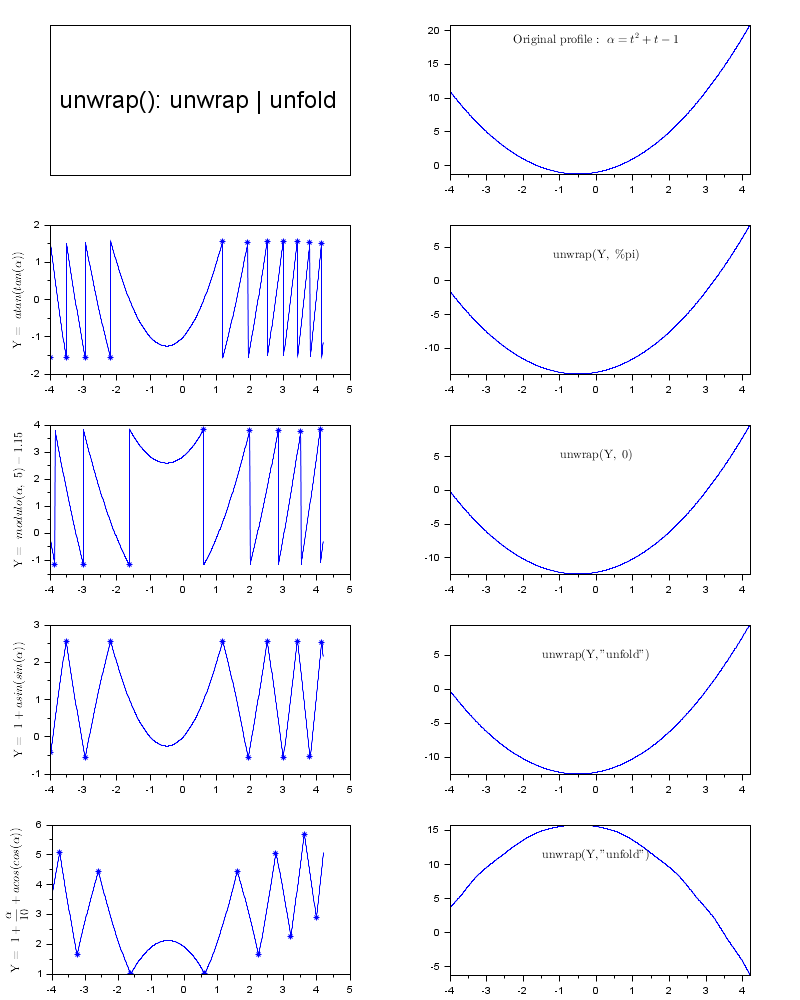
2次元面をアンラップ:
// 2次元の例 // ----------- ax = gda(); ax.title.font_size = 2; f = scf(); f.color_map = hotcolormap(100); f.figure_size = [475 1050]; f.figure_position(2) = 0; f.figure_name = "unwrap()" + _(": 2-D examples"); drawlater() nx = 300; ny = 400; rmax = 8.8; x = linspace(-rmax/2, rmax/2, nx)-1; y = linspace(-rmax/2, rmax/2, ny)+1; [X, Y] = meshgrid(x,y); for ex=0:1 // 例 // 元の面 // 面を生成 if ex==0 then z = X.^2 + Y.^2; else z = sqrt(0.3+sinc(sqrt(z)*3))*17-7; end // 3次元でプロットします subplot(4,2,1+ex) surf(x, y, z) title("Original profile Z") e = gce(); e.thickness = 0; // メッシュを削除 e.parent.tight_limits = "on"; // ラップされた面 (平面) m = 2.8; zw = pmodulo(z, m); // ラップする subplot(4,2,3+ex) grayplot(x, y, zw') title(msprintf("Zw = pmodulo(Z, %g) (flat)",m)) ax0 = gca(); ax0.tight_limits = "on"; // アンラップされた面 (平面): // in both directions: u = unwrap(zw, 0); subplot(4,2,5+ex) grayplot(x, y, u') title(msprintf("unwrap(Zw, %g) (flat)", 0)) ax3 = gca(); ax3.tight_limits = "on"; if ex==0 then direc = "r"; else direc = "c"; end // 一方向にアンラップ: u = unwrap(zw, m, direc); subplot(4,2,7+ex) grayplot(x, y, u') title(msprintf("unwrap(Zw, %g, ""%s"") (flat)",m,direc)) ax1 = gca(); ax1.tight_limits = "on"; end sda(); drawnow()
履歴
| Version | Description |
| 5.5.0 | unwrap() 関数が導入されました |
| Report an issue | ||
| << triu | matrixoperations | searchandsort >> |