Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
cumsum
配列要素の累積和
呼び出し手順
y=cumsum(x) y=cumsum(x,orientation) y=cumsum(x,outtype) y=cumsum(x,orientation,outtype)
引数
- x
実数,複素数,論理値,多項式または有理数の配列
- orientation
以下のどちらかを指定します
文字列で,指定可能な値は
"*","r","c"または"m"正の整数値
- outtype
文字列で,指定可能な値は
"native"または"double".- y
スカラーまたは配列
説明
xは配列の場合,y=cumsum(x) は,
xの全要素の累積和を
スカラーyに返します:
y=cumsum(x,orientation) は
orientationにより指定された次元方向の
x の累積和をyに返します:
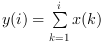
orientation が 1 または "r" の場合:
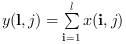
または
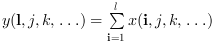
orientation が 2 または "c" の場合:
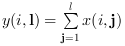
または
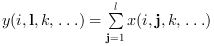
orientation が n の場合:
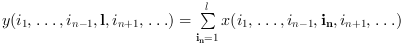
y=cumsum(x,"*")はy=cumsum(x)と等価です.y=cumsum(x,"m")はy=cumsum(x,orientation)と等価です. ただし,orientationは xの1より大きい最初の次元の添字です. このオプションはMatlabとの互換性のために使用されます.
outtype引数は総和の動作を指定します:
float, 多項式 有理数の配列の場合, 評価は浮動小数点演算により 行われます.
"double"または"native"オプションは等価です.整数の配列の場合,
outtype="native"の時, 評価は整数演算(モジュロ 2^b, ただし b は使用されるビット数)で行われます,outtype="double"の時,評価は浮動小数点演算により 行われます.デフォルト値は
outtype="native"です.論理値の配列の場合,
outtype="native"の時,評価は論理値演算 (+ は | で置換)により行われます,outtype="double"の時,評価は 浮動小数点演算(%t は 1, %f は 0で置換)により行われます.デフォルト値は
outtype="double"です.
 | This function applies with identical rules to sparse matrices |
例
| Report an issue | ||
| << cumprod | matrixoperations | kron >> |