Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
cdfnor
fonction de répartition de la distribution normale
Séquence d'appel
[P,Q]=cdfnor("PQ",X,Mean,Std) [X]=cdfnor("X",Mean,Std,P,Q) [Mean]=cdfnor("Mean",Std,P,Q,X) [Std]=cdfnor("Std",P,Q,X,Mean)
Paramètres
- P,Q,X,Mean,Std
six vecteurs réels de même taille.
- P,Q (Q=1-P)
L'intégrale de -infini à X de la densité normale En entrée : (0,1].
- X
Borne supérieure d'intégration En entrée : ( -infini, +infini)
- Mean
moyenne de la densité En entrée : (-infini, +infini)
- Sd
écart-type de la densité En entrée : (0, +infini).
Description
Étant donnés les autres, calcule un paramètre de la distribution normale.
Une version légèrement modifiée de ANORM :
Cody, W.D. (1993). "ALGORITHM 715: SPECFUN - A Portable FORTRAN Package of Special Function Routines and Test Drivers" acm Transactions on Mathematical Software. 19, 22-32.
est utilisée.
Les fonctions rationnelles des pages 90-95 de
Kennedy and Gentle, Statistical Computing, Marcel Dekker, NY, 1980
sont utilisées comme valeurs de départ pour les itérations de Newton calculant l'inverse de la distribution. Aucune recherche n'est donc nécessaire pour aucun des paramètres.
Pour X < -15, le développement asymptotique de la loi normale est utilisé comme valeur de départ pour trouver l'inverse. Il s'agit de la formule 26.2.12 de Abramowitz et Stegun.
La densité normale est proportionnelle à exp( - 0.5 * (( X - MEAN)/SD)**2)
Tiré de la bibliothèque DCDFLIB: Library of Fortran Routines for Cumulative Distribution Functions, Inverses, and Other Parameters (February, 1994) Barry W. Brown, James Lovato and Kathy Russell. The University of Texas.
Exemples
// Calculer p à partir de x x = -1; Mean = 0; Std = 1; // P = 0.1586553, Q = 0.8413447 [P,Q]=cdfnor("PQ",x,Mean,Std)
// Calculer p à partir d'un x très rare // Noter que Q doit être utilisé lorsque P est proche de 1, // alors que P doit être utilisé lorsque Q est proche de 1. x = 10; Mean = 0; Std = 1; // P = 1, Q = 7.620D-24 [P,Q]=cdfnor("PQ",x,Mean,Std)
// Créer une table de P,Q Mean = 0; Std = 1; x = -6:6; [P,Q]=cdfnor("PQ",x,Mean*ones(x),Std*ones(x)); [x' P' Q']
// Trouver x à partir de p,q Mean = 0; Std = 1; p = 0.1; q = 0.9; // x = - 1.2815516 x = cdfnor("X",Mean,Std,p,q)
// Trouver Mean à partir de p,q x = 2; Std = 1; p = 0.1; q = 0.9; // Mean = 3.2815516 Mean = cdfnor("Mean",Std,p,q,x)
// Trouver l'écart-type Std à partir p,q Mean = 0; p = 0.1; q = 0.9; x = 2; // Std = - 1.5606083 Std = cdfnor("Std",p,q,x,Mean)
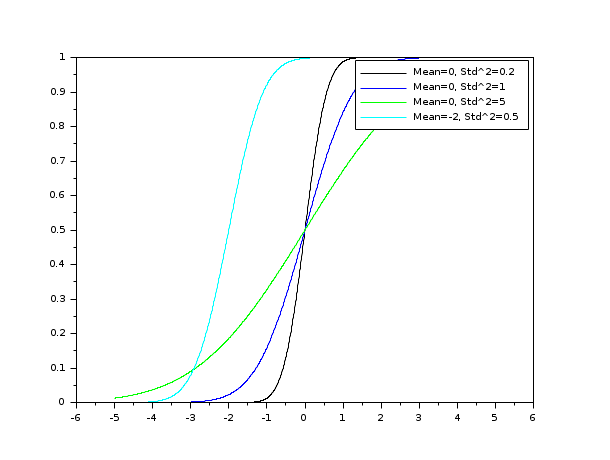
// Afficher la fonction h = scf(); Mean = [0 0 0 -2]; Std2 = [0.2 1.0 5.0 0.5]; cols = [1 2 3 4]; nf = size(cols,"*"); lgd = []; for k = 1 : nf x = linspace(-5,5,1000); P=cdfnor("PQ",x,Mean(k)*ones(x),sqrt(Std2(k))*ones(x)); plot(x,P) str = msprintf("Mean=%s, Std^2=%s",string(Mean(k)),string(Std2(k))); lgd($+1) = str; end for k = 1 : nf h.children.children.children(nf - k + 1).foreground = cols(k); end legend(lgd);
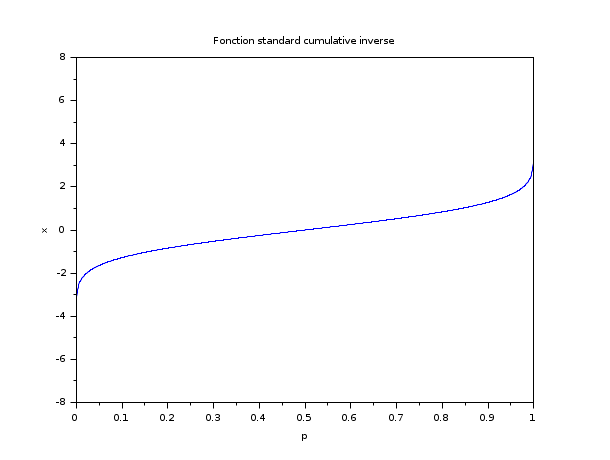
// Afficher la fonction fonction standard cumulative inverse Mean = 0; Std = 1; p = linspace(1e-10,1-1e-10,1000); q = 1-p; x = cdfnor("X",Mean*ones(p),Std*ones(p),p,q); plot(p,x) xtitle("Fonction standard cumulative inverse","p","x");
// La fonction Inverse Normale CDF est mal conditionnée lorsque // p est proche de p=0.5. // Ceci parce-que, à p=0.5, la première dérivée est non nulle, // mais la fonction est nulle. // Ceci peut produire une erreur relative très large dans la fonction, // c'est-à-dire que des décimales sont susceptibles d'êtres de plus en plus fausses // lorsque p s'approche de p=0.5. Mean = 0; Std = 1; p = 0.500000001; q = 1-p; x = cdfnor("X",Mean,Std,p,q) // La probabilité attendue a été calculée dans un software symbolique, // avec l'expression sqrt(2)*erfinv(2*p-1) // où p = 1/2+10^-9. expected = 2.50662827463100050e-9; // L'erreur relative est d'environ 1.e-8, ce qui veut dire que // seulement 8 décimales sont correctes. abs(x-expected)/abs(expected)
// L'agorithme de traversée de zéro peut être incapable de déterminer l'écart-type // dans certaines situations, quand l'inversion ne peut pas avoir lieu. Mean = 1; p = 0.5; q = 0.5; x = 1; // Std = Nan Std = cdfnor("Std",p,q,x,Mean)
Voir aussi
- cdfbet — fonction de répartition de la distribution Beta
- cdfbin — fonction de répartition de la distribution binomiale
- cdfchi — fonction de répartition de la distribution du chi-deux
- cdfchn — fonction de répartition de la distribution du chi-deux non centrée
- cdff — fonction de répartition de la distribution de Fisher
- cdffnc — fonction de répartition de la distribution de Fisher non centrée
- cdfgam — fonction de répartition de la distribution gamma
- cdfnbn — fonction de répartition de la distribution binomiale négative
- cdfpoi — fonction de répartition de la distribution de Poisson
- cdft — fonction de répartition de la distribution de Student
| Report an issue | ||
| << cdfnbn | Cumulated Distribution Functions | cdfpoi >> |