- Scilab help
- CACSD (Computer Aided Control Systems Design)
- Formal representations and conversions
- Plot and display
- abinv
- arhnk
- arl2
- arma
- arma2p
- arma2ss
- armac
- armax
- armax1
- arsimul
- augment
- balreal
- bilin
- bstap
- cainv
- calfrq
- canon
- ccontrg
- cls2dls
- colinout
- colregul
- cont_mat
- contr
- contrss
- copfac
- csim
- ctr_gram
- damp
- dcf
- ddp
- dhinf
- dhnorm
- dscr
- dsimul
- dt_ility
- dtsi
- equil
- equil1
- feedback
- findABCD
- findAC
- findBD
- findBDK
- findR
- findx0BD
- flts
- fourplan
- freq
- freson
- fspec
- fspecg
- fstabst
- g_margin
- gamitg
- gcare
- gfare
- gfrancis
- gtild
- h2norm
- h_cl
- h_inf
- h_inf_st
- h_norm
- hankelsv
- hinf
- imrep2ss
- inistate
- invsyslin
- kpure
- krac2
- lcf
- leqr
- lft
- lin
- linf
- linfn
- linmeq
- lqe
- lqg
- lqg2stan
- lqg_ltr
- lqr
- ltitr
- macglov
- minreal
- minss
- mucomp
- narsimul
- nehari
- noisegen
- nyquistfrequencybounds
- obs_gram
- obscont
- observer
- obsv_mat
- obsvss
- p_margin
- parrot
- pfss
- phasemag
- plzr
- pol2des
- ppol
- prbs_a
- projsl
- reglin
- repfreq
- ric_desc
- ricc
- riccati
- routh_t
- rowinout
- rowregul
- rtitr
- sensi
- sident
- sorder
- specfact
- ssprint
- st_ility
- stabil
- sysfact
- syslin
- syssize
- time_id
- trzeros
- ui_observer
- unobs
- zeropen
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
arma
Scilab arma library
Description
Armax processes can be coded with Scilab tlist of type 'ar'.
armac is used to build Armax scilab object. An 'ar'
tlist contains the fields ['a','b','d','ny','nu','sig'].
- armac
this function creates a Scilab tlist which code an Armax process
A(z^-1)y= B(z^-1)u + D(z^-1)sig*e(t)-->ar=armac([1,2],[3,4],1,1,1,sig); -->ar('a') ans = ! 1. 2. ! -->ar('sig') ans = 1.
- armap(ar [,out])
Display the armax equation associated with
ar- armap_p(ar [,out])
Display the armax equation associated with
arusing polynomial matrix display.- [A,B,D]=armap2p(ar)
extract polynomial matrices from ar representation
- armax
is used to identify the coefficients of a n-dimensional ARX process
A(z^-1)y= B(z^-1)u + sig*e(t)- armax1
armax1 is used to identify the coefficients of a 1-dimensional ARX process
A(z^-1)y= B(z^-1)u + D(z^-1)sig*e(t)- arsimul
armax trajectory simulation.
- narsimul
armax simulation ( using rtitr)
- odedi
Simple tests of ode and arsimul. Tests the option 'discret' of ode
- prbs_a
pseudo random binary sequences generation
- reglin
Linear regression
Example
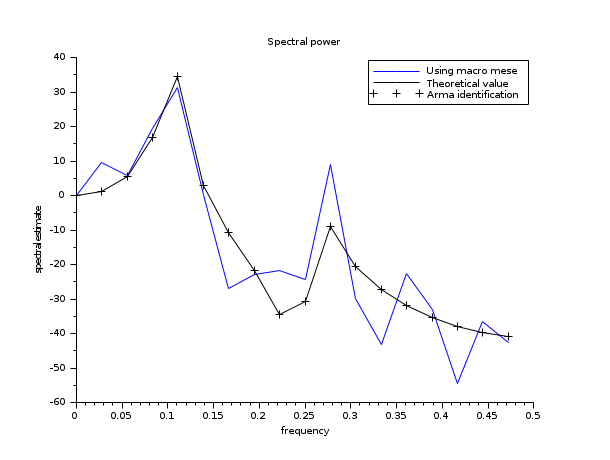
// Example extracted from the demo arma3.dem.sce in the cacsd module // Spectral power estimation // ( form Sawaragi et all) m = 18; a = [1,-1.3136,1.4401,-1.0919,+0.83527]; b = [0.0,0.13137,0.023543,0.10775,0.03516]; u = rand(1,1000,'n'); z = arsimul(a,b,[0],0,u); //----Using macro mese [sm,fr]=mese(z,m); //----The theorical result function gx=gxx(z, a, b) w = exp(-%i*2*%pi*z*(0:4))' gx = abs(b*w)^2/(abs(a*w)^2); endfunction res=[]; for x=fr res=[ res, gxx(x,a,b)]; end //----using armax estimation of order (4,4) // it's a bit tricky because we are not supposed to know the order [arc,la,lb,sig,resid]=armax(4,4,z,u); res1=[]; for x=fr res1=[ res1, gxx(x,la(1),lb(1))]; end //-- visualization of the results plot2d([fr;fr;fr]',[20*log10(sm/sm(1));20*log10(res/res(1));20*log10(res1/res1(1))]',[2,1,-1]) legend(["Using macro mese";"Theoretical value";"Arma identification"]) xtitle("Spectral power","frequency","spectral estimate")
| Report an issue | ||
| << arl2 | CACSD (Computer Aided Control Systems Design) | arma2p >> |