Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes
Scilab Online Help
2025.0.0 - Français


dae

Solveur de système d'Equations Différentielles Algébriques

Séquence d'appel

y = dae(y0, t0, t, res)
[y [,hd]] = dae(y0, t0, t [[,rtol], atol], res [,jac] [,hd])

[y, rd] = dae("root", y0, t0, t, res, ng, surface)
[y, rd [,hd]] = dae("root", y0, t0, t [[,rtol], atol], res [,jac], ng, surface [,hd])

[y, rd] = dae("root2", y0, t0, t, res, ng, surface)
[y, rd [,hd]] = dae("root2", y0, t0, t [[,rtol], atol], res [,jac], ng, surface [, psol, pjac] [, hd])

y = dae("stiff"|"adams", y0, t0, t, res, adda)
[y [,hd]] = dae("stiff"|"adams", y0, t0, t [[,rtol], atol], res [,jac], adda [,hd])

Paramètres

y0

vecteur colonne ou matrix. Peut valoir x0 ou [x0, xdot0], où x0 est la valeur de l'état au temps initial t0 et xdot0 est la valeur (ou une estimation) de l'état dérivé au temps initial (voir ci-après).

t0

réel, le temps initial.

t

scalaire ou vecteur réel. Les instants auxquels la solution est voulue. La solution peut s'obtenir à chaque étape de dae en initialisant %DAEOPTIONS(2)=1 .

rtol

un scalaire ou vecteur colonne réel de même taille que x0, la tolérance relative de la solution. Si atol est un vecteur, les tolérances sont spécifiées pour chaque composante de l'état.

atol

un scalaire ou vecteur colonne réel de même taille que x0, la tolérance absolue de la solution. Si atol est un vecteur, les tolérances sont spécifiées pour chaque composante de l'état.

res

une fonction external, calcule la valeur de g(t, y, ydot). Peut être une fonction, liste ou chaîne de caractères. La syntaxe diffère en fonction du solveur utilisé. Pour plus d'informations, voir la section description "résidu".

jac

une fonction external, calcule la valeur Jacobien de la fonction g(t, y, ydot). Elle peut être une fonction, liste ou chaîne de caractères. La syntaxe diffère en fonction du solveur utlisé. Pour plus de détails, voir la section ci-dessous "decription jacobien"

surface

une fonction external (fonction, liste ou chaîne de caratères), calcule a valeur du vecteur colonne surface(t,x) à ng éléments. Chaque élément définit une surface. Utilisée uniquement avec les solveurs dasrt ("root") and daskr ("root2"). Pour plus d'informations, voir la section "description surface"

adda

une fonction external (fonction, liste ou chaîne de caratères), calcule p = p + a avec a = a(t,y). Utilisée uniquement avec les solveurs stiff and adams. Pour plus d'informations, voir la section "description adda".

psol

external (fonction, liste ou chaîne de caractères). Utilisée uniquement avec le solveur "root2" (daskr). Résout le système linéaire P*x=b, avec P le préconditionneur factorisé que la routine pjac a calculé et stocké dans wp et iwp. Voir la section de description de psol pour plus de détails.

pjac

external (fonction, liste ou chaîne de caractères). Utilisée uniquement avec le solveur "root2" (daskr). Calcule la valeur de dg/dy + cj*dg/dydot pour une valeur donnée du paramètre cj et la factorise en LU dans deux tableaux, réel et entier. Voir la section de description de pjac pour plus de détails.

y

matrice réelle. Si %DAEOPTIONS(2)=1 , chaque colonne est le vecteur [t;x(t);xdot(t)] où t est le temps auquel la solution à été calculée. Sinon y est le vecteur [x(t);xdot(t)].

rd

un vecteur à deux entrées [times num] où times est la valeur des temps auquel les surfaces sont traversées, num est le nombre de surfaces traversées.

hd

vecteur réel, stocke en sortie le contexte de dae. Peut être utilisé comme paramètre d'entrée pour reprendre l'intégration (reprise à chaud).

Description

La fonction dae résout l'équation différentielle algébrique et renvoie l'évolution de y à des moments donnés

g(t, x, xdot) = 0
x(t0) = x0 and xdot(t0) = xdot0

Si xdot0 n'est pas donné en paramètre initial, dae tente de la calculer en résolvant g(t,x0,xdot0)=0.

Si xdot0 est donné en paramètre initial, il peut soit satifaire g(t,x0,xdot0)=0, soit en être une approximation. Dans le dernier cas, %DAEOPTIONS(7) doit être initialisé à 1.

Les solveurs

Le type de problème résolu et la méthode utilisée dépendent de la valeur du premier argument optionnel type qui peut être l'une des chaînes suivantes :

<non donné>:

le solveur dassl.

"root":

le solveur dasrt. Voir l'aide dae_root pour plus de détails.

"root2":

le solveur daskr. Voir l'aide dae_root pour plus de détails.

"adams":

Pour les problèmes non rigides. Le solveur lsodi du package ODEPACK est appelé et utilise la méthode Adams.

"stiff":

Pour les problèmes rigides. Le solveur lsodi du package ODEPACK est appelé et utilise la méthode BDF.

Fonction résidu

L'argument d'entrée res retourne le résidu du DAE. C'est un external c'est-à-dire soit une fonction avec une syntaxe spécifique, soit un nom de la fonction Fortran ou C, soit une liste. La séquence d'appel de la fonction diffère selon le solveur utilisé quand res est une chaîne de caractère.

une fonction Scilab

Dans ce cas, la séquence d'appel doit être

[r, ires] = res(t, y, ydot)

où res doit retourner le résidu et le drapeau d'erreur ires.

ires = 0 si res est bien parvenu à calculer r.

ires = -1 so le résidu est localement non-défini pour g(t, x, xdot).

ires =-2 si les paramètres sont hors de la plage admissible.

Si le solveur adams ou stiff est utilisé, cette fonction doit retourner r = g(t,y)-A(t,y)*ydot

une liste

Cette forme permet de passer des paramètres à la fonction. Elle doit se présenter comme suit:

list(res, p1, p2, ...)

où la séquence d'appel de la fonction res est

r = res(t, y, ydot, p1, p2, ...)

res retourne toujours le résidu comme fonction de (t, x, xdot, x1, x2, ...), et p1, p2,... sont des paramètres de la fonction.

une chaîne de caractère

Elle doit se référer au nom d'une routine C ou Fortran. En fonction du solveur, la séquence d'appel est différente. Supposant que <r_name> est le nom donné,

Si le solveur dassl, dasrt ("root") ou daskr ("root2") est utilisé, res peut être

  • La séquence d'appel en Fortran doit être

    subroutine <r_name>(t, x, xdot, res, ires, rpar, ipar)
double precision t, x(*), xdot(*), res(*), rpar(*)
integer ires, ipar(*)

  • La séquence d'appel en C doit être

    void <r_name>(double *t, double *x, double *xdot, double *res, int *ires, double *rpar, int *ipar)

où

  • t est la valeur actuelle du temps

  • x est la valeur de l'état

  • xdot est la valeur de l'état dérivé

  • res la valeur du résidu

  • ires indicateur de complétion

  • rpar est un vecteur de paramètres nécéssaires mais non initialisables par dae.

  • ipar est un vecteur de paramètres entiers nécéssaires mais non initialisables par dae

Si le solveur adams ou stiff est utilisé, res peut être

  • La séquence d'appel en Fortran doit être

    subroutine <r_name>(neq, t, x, xdot, res, ires)
double precision t, x(*), xdot(*), res(*)
integer neq, ipar(*)

  • La séquence d'appel en C doit être

    void <r_name>(int *neq, double *t, double *x, double *xdot, double *res, int *ires)

où

  • neq est le nombre d'équation du système

  • t est la valeur actuelle du temps

  • x est la valeur de l'état

  • xdot est la valeur de l'état dérivé

  • res la valeur du résidu

  • ires indicateur de complétion

La fonction jacobienne

L'arugment d'entrée jac calcule le jacobien. Comme res, jac est un external c'est-à-dire soit une fonction avec une syntaxe spécifique, soit un nom de la fonction Fortran ou C, soit une liste. La séquence d'appel de la fonction diffère selon le solveur utilisé.

Si le solveur dassl, dasrt ("root") ou daskr ("root2") est utilisé, jac calcule la valeur de dg/dx + cj * dg/dxdot pour une valeur donnée du paramètre cj. Elle peut être

une fonction Scilab

Dans ce cas, sa séquence d'appel doit être

j = jac(t, y, ydot, cj)

où la fonction jac doit retourner

j = dg(t, x, xdot)/dy + cj * dg(t, x, xdot)/dxdot

où cj est une réel scalaire.

une liste

Cette forme d'external sert à p asser des paramètres à la fonction. Elle doit se présenter comme suit::

list(jac, p1, p2, ...)

où la séquence d'appel de la fonction jac est

r = jac(t, x, xdot, cj, p1, p2, ...)

jac retourne toujours dg/dx+cj*dg/dxdot comme fonction de (t,x,xdot,cj,p1,p2,...).

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran. Supposant que <j_name> est le nom donné,

  • La séquence d'appel en Fortran doit être

    subroutine <j_name>(t, x, xdot, r, cj, ires, rpar, ipar)
double precision t, x(*), xdot(*), r(*), cj, rpar(*)
integer ires, ipar(*)

  • La séquence d'appel en C doit être

    void <j_name>(double *t, double *x, double
*xdot, double *r, double *cj, int *ires, double *rpar, int *ipar)

où t, x, xdot, ires, rpar, ipar ont une définition similaire à celle ci-dessus, r est le tableau de résultats.

Pour les solveurs adams et stiff, jac peut être

une fonction Scilab

Dans ce cas, sa séquence d'appel doit être

j = jac(t, y, ydot)

où la fonction jac doit retourner le Jacobien de r = g(t,y)-A(t,y)*ydot par rapport à y.

une liste

Cette forme d'external sert à passer des paramètres à la fonction. Elle doit se présenter comme suit::

list(jac, p1, p2, ...)

où la séquence d'appel de la fonction jac est

r = jac(t, y, ydot, p1, p2, ...)

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran. Supposant que <j_name> est le nom donné,

  • La séquence d'appel en Fortran doit être

    subroutine <j_name>(neq, t, x, xdot, ml, mu, j, nrpd)
double precision t, x(*), xdot(*), j(*)
integer neq, ml, mu, nrpd

  • La séquence d'appel en C doit être

    void <j_name>(int *neq, double *t, double *x, double *xdot, int *ml, int *mu, double *j, int *nrpd)

la fonction surface

L'argument d'entrée surface, utilisé seulement avec les solveurs dassl, dasrt ("root") et daskr ("root2"), calcule la valeur du vecteur colonne surface(t,x) avec ng éléments. Chaque élément définit une surface. Comme res, surface est une fonction external qui peut être

une fonction Scilab

Sa séquence d'appel doit être

r=surface(t,x)

cette fonction doit retourner un vecteur colonne à ng éléments.

une liste

Cette forme d'external est utilisée pour passer des paramètres à la fonction. Elle doit se présenter comme suit:

list(surface,p1,p2,...)

où la séquence d'appel de la fonction surface est

r = surface(t,x,p1,p2,...)

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran. Supposant que <s_name> est le nom donné,

  • La séquence d'appel en Fortran doit être

    subroutine <s_name>(nx, t, x, ng, r, rpar, ipar)
double precision t, x(*), r(*), rpar(*)
integer nx, ng,ipar(*)

  • La séquence d'appel en C doit être

    void <s_name>(int *nx, double *t, double *x, int *ng, double *r, double *rpar, int *ipar)

où t, x, rpar, ipar ont les mêmes définitions qu'au-dessus, ng est le nombre de surfaces, nx est la dimension de l'état et r est le vecteur résultat.

la fonction adda

l'argument d'entrée adda, utilisé uniquement avec les solveurs adams et stiff, calcule r = A(t,y) + p où p est une matrice à ajouter à A(t,y). Comme res, adda est une fonction external. Elle peut être

une fonction Scilab

Sa séquence d'appel doit être

r=adda(t, y, p)

une liste

Cette forme d'external sert à passer des paramètres à la fonction. Elle doit se présenter comme suit:

list(adda,p1,p2,...)

où la séquence d'appel de la fonction adda est

adda(t,x,p1,p2,...)

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran. Supposant que <a_name> est le nom donné,

  • La séquence d'appel en Fortran doit être

    subroutine <a_name>(nx, t, x, ml, mu, p, nrpd)
double precision t, x(*), p(*)
integer nx, ml, mu, nrpd

  • La séquence d'appel en C doit être

    void <a_name>(int *nx, double *t, double *x, int *ml, int *mu, double *p, int *nrpd)

Dans la plupart des cas, vous n'êtes pas obligé de référer ml, mu and nrpd.

la function psol

L'argument d'entrée psol, utilisé uniquement avec le solveur daskr, résout le système linéaire P*x = b Comme res, psol est une fonction external. Elle peut être

une fonction Scilab

Sa séquence d'appel doit être

[r, ier] = psol(wp, iwp, b)

et doit renvoyer la solution du système dans r et l'indicateur d'erreur ier.

une liste

Cette forme d'external sert à passer des paramètres à la fonction. Elle doit se présenter comme suit:

list(psol,p1,p2,...)

où la séquence d'appel de la fonction psol est

psol(wp, iwp, b, x1, x2, ...)

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran

  • La séquence d'appel en Fortran doit être

    subroutine psol (neq, t, y, ydot, savr, wk, cj, wght, wp, iwp, b, eplin, ier, rpar, ipar)
double precision t,y(*), ydot(*), savr(*), wk(*), cj, wght(*), wp(*), b(*), eplin, rpar(*)
integer neq, iwp(*), ier, ipar(*)

  • La séquence d'appel en C doit être

    void psol (int*neq, double*t, double*y, double*ydot, double*savr, double*wk, double*cj, double*wght, double*wp, int*iwp, double*b, double*eplin, int*ier, double*rpar, int*ipar)

la fonction pjac

L'arugment d'entrée pjac, utilisé uniquement avec le solveur daskr, calcule la valeur de dg/dy + cj*dg/dydot pour une valeur donnée du paramètre cj et le factorise(LU) en deux vecteurs, réel et entier. Comme res, psol est une fonction external. Elle peut être

une fonction Scilab

Sa séquence d'appel doit être

[wp, iwp, ires] = pjac(neq, t, y, ydot, h, cj, rewt, savr)

les vecteurs wp et iwp doivent contenir toutes les informations pondérées sur le préconditionneur.

une liste

Elle doit se présenter comme suit:

list(pjac, x1, x2,...)

où la séquence d'appel de la fonction pjac est

pjac(neq, t, y, ydot, h, cj, rewt, savr, x1, x2,...)

pjac retourne toujours dg/dy + cj*dg/dydot comme fonction de (neq, t, y, ydot, h, cj, rewt, savr, x1, x2, ...).

une chaîne de caractères

Elle doit se référer au nom d'une routine C ou Fortran

  • La séquence d'appel en Fortran doit être

    subroutine pjac (res, ires, neq, t, y, ydot, rewt, savr, wk, h, cj, wp, iwp, ier, rpar, ipar)
double precision res(*), t, y(*), ydot(*), rewt(*), savr(*),  wk(*), h, cj, wp(*), rpar(*)
integer ires, neq, iwp(*), ier, ipar(*)

  • La séquence d'appel en C doit être

    void pjac (double*res, int*ires, int*neq, double*t, double*y, double*ydot, double*rewt, double*savr, double*wk, double*h, double*cj, double*wp, int*iwp, int*ier, double*rpar, int*ipar)

Exemples

Exemple #1: dassl (pas de traversée de surface)

// Exemple avec du code Scilab
//--------------------------------------------------
function [r, ires]=chemres(t, y, yd)
    r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1);
    r(2) =  0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2);
    r(3) =       y(1) +     y(2)      + y(3)-1;
    ires =  0;
endfunction

function pd=chemjac(x, y, yd, cj)
    pd = [-0.04-cj , 1d4*y(3)               , 1d4*y(2);
           0.04    ,-1d4*y(3)-2*3d7*y(2)-cj ,-1d4*y(2);
           1       , 1                      , 1       ]
endfunction

x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400, 4000, 40000, 4d5, 4d6, 4d7, 4d8, 4d9, 4d10];

y = dae([x0, xd0], 0, t, chemres); // Retourne les points d'observation demandés

%DAEOPTIONS = list([], 1, [], [], [], 0, 0); // Demande à dae les points à retourner
y = dae([x0, xd0], 0, 4d10, chemres); // Sans jacobian
y = dae([x0, xd0], 0, 4d10, chemres, chemjac); // Avec jacobien

Exemple #2: utilise le solveur dasrt avec "root"

// Exemple avec du code C (compilateur C requis)
//--------------------------------------------------
bOK = haveacompiler();
if bOK <> %t
    [btn] = messagebox(["Vous avez besoin d''un compilateur C pour cet exemple."; "Arrêt de l''exécution."], "Problème de Software", "info");
    return
end

//-1- Crée les codes C dans TMPDIR - équation de Vanderpol, forme implicite
code = ['#include <math.h>'
      'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)'
      '{res[0] = yd[0] - y[1];'
      ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}'
      ' '
      'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)'
      '{pd[0] = *cj - 0.0;'
      ' pd[1] =     - (-200.0*y[0]*y[1] - 1.0);'
      ' pd[2] =     - 1.0;'
      ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}'
      ' '
      'void gr22(int *neq, double *t, double *y, int *ng, double *groot, double *rpar, int *ipar)'
      '{ groot[0] = y[0];}']
previous_dir = pwd();
cd TMPDIR;
mputl(code, 't22.c')

//-2- Compile et charge
ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce');
exec('t22loader.sce')

//-3- Exécute
rtol = [1.d-6; 1.d-6];
atol = [1.d-6; 1.d-4];
t0 = 0; t = [20:20:200];
y0 = [2; 0]; y0d = [0; -2];
ng = 1;

// Simulation simple
t = 0:0.003:300;
yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22');
clf(); plot(yy(1, :), yy(2, :))
// Trouve le premier point où yy(1) = 0
[yy, nn, hotd] = dae("root", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22');
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));

// Reprise à chaud pour le point suivant
t01 = nn(1);
[pp, qq] = size(yy);
y01 = yy(2:3, qq); y0d1 = yy(3:4, qq);
[yy, nn, hotd] = dae("root", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', hotd);
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));
cd(previous_dir);

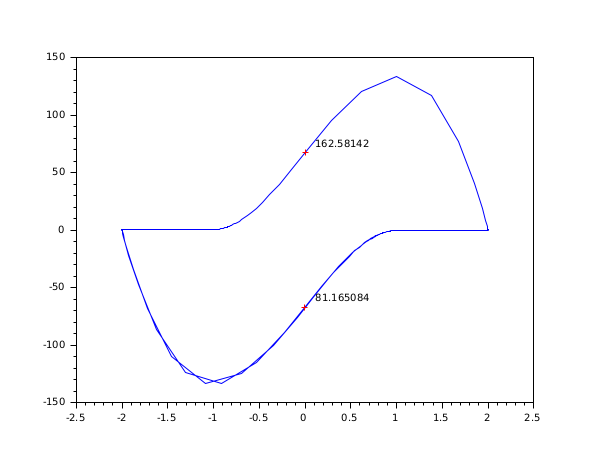
Exemple #3: utilise le solveur daskr avec le mot-clé "root2", avec les routines 'psol' et 'pjac' par défaut

// Exemple avec du code C (compilateur C requis)
//--------------------------------------------------
bOK = haveacompiler();
if bOK <> %t
    [btn] = messagebox(["Vous avez besoin d''un compilateur C pour cet exemple."; "Arrêt de l''exécution."], "Problème de Software", "info");
    return
end

//-1- Crée les codes C dans TMPDIR - équation de Vanderpol, forme implicite
code = ['#include <math.h>'
      'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)'
      '{res[0] = yd[0] - y[1];'
      ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}'
      ' '
      'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)'
      '{pd[0] = *cj - 0.0;'
      ' pd[1] =     - (-200.0*y[0]*y[1] - 1.0);'
      ' pd[2] =     - 1.0;'
      ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}'
      ' '
      'void gr22(int *neq, double *t, double *y, double *yd, int *ng, double *groot, double *rpar, int *ipar)'
      '{ groot[0] = y[0];}']
previous_dir = pwd();
cd TMPDIR;
mputl(code, 't22.c')

//-2- Compile et charge
ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce');
exec('t22loader.sce')

//-3- Exécute
rtol = [1.d-6; 1.d-6];
atol = [1.d-6; 1.d-4];
t0 = 0; t = [20:20:200];
y0 = [2; 0]; y0d = [0; -2];
ng = 1;

// Simulation simple
t = 0:0.003:300;
yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22');
clf(); plot(yy(1, :), yy(2, :))
// Trouve le premier point où yy(1) = 0
%DAEOPTIONS = list([] , 0, [], [], [], 0, [], 1, [], 0, 1, [], [], 1);
[yy, nn, hotd] = dae("root2", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1');
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));

// Reprise à chaud pour le point suivant
t01 = nn(1);
[pp, qq] = size(yy);
y01 = yy(2:3, qq); y0d1 = yy(3:4, qq);
[yy, nn, hotd] = dae("root2", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1', hotd);
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));
cd(previous_dir);

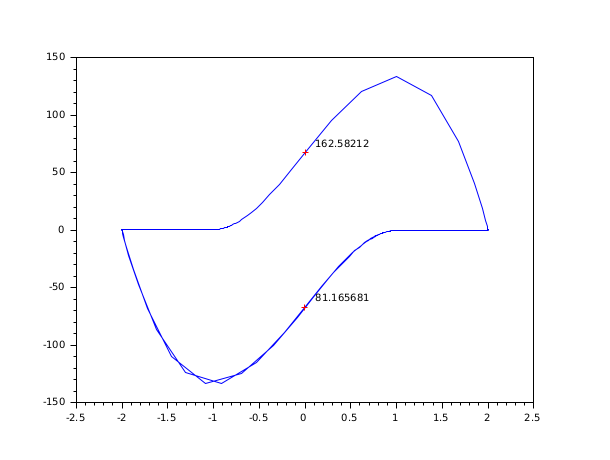
Exemple #4: utilise le solveur stiff

// Exemple avec le code Scilab
//--------------------------------------------------
function [r, ires]=chemres(t, y, yd)
r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1);
r(2) =  0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2);
r(3) =       y(1) +     y(2)      + y(3)-1;
ires =  0;
endfunction

function j=chemjac(t, y, yd)
j = [-0.04 , 1d4*y(3)               , 1d4*y(2);
0.04    ,-1d4*y(3)-2*3d7*y(2) ,-1d4*y(2);
1       , 1                      , 1       ]
endfunction

function p=addap(t, y, p)
    p(1,1) = p(1,1) + 1;
    p(2,2) = p(2,2) + 1;
endfunction

x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400];

y = dae("stiff", [x0, xd0], 0, 300, chemres, addap);
y = dae("stiff", [x0, xd0], 0, 300, chemres, chemjac, addap); // avec le jacobien

Exemple #5: utilise le solveur stiff solver avec du code compilé

//-1- Crée les codes C dans TMPDIR
code = ['#include <math.h>'
  'void chemres(int *neq, double *t, double *y, double *s, double *res, int *ires, double *rpar, int *ipar)'
  '{res[0] = -0.040*y[0] + 1.0e4*y[1]*y[2] - s[0];'
  ' res[1] = 0.040*y[0] - 1.0e4*y[1]*y[2] - 3.0e7*y[1]*y[1] - s[1];'
  'res[2] = y[0] + y[1] + y[2] - 1.0;}'
  ' '
  'void chemjac(double *t, double *y, double *s, double *ml, double *mu, double *p, int *nrowp)'
  '{p[0] = -0.04;'
  ' p[1] = 0.040;'
  ' p[2] = 1.0;'
  'p[3] = 1.0e4*y[2];'
  ' p[4] = -1.0e4*y[2] - 6.0e7*y[1];'
  ' p[5] = 1.0;'
  'p[6] = 1.0e4*y[1];'
 ' p[7] = -1.0e4*y[1];'
 ' p[8] = 1.0;}'
  ' '
  'void addap(int *neq, double *t, double *y, double *ml, double *mu, double *p, int *nrowp)'
  '{ p[0] = p[0] + 1.0;'
  'p[4] = p[4] + 1.0;'
  '}']

mputl(code, fullfile(TMPDIR, 'mydae.c'))

//-2- Compile et charge
cd TMPDIR
ilib_for_link(['chemres' 'chemjac' 'addap'], 'mydae.c', [], 'c', [], 'loader.sce');
exec('loader.sce')

//-3- Simulation simple
rtol = [1d-6; 1d-6; 1d-6];
    atol = [1d-6; 1d-6; 1d-4];
    t0 = 0;
    x0 = [1; 0; 0];
    xd0 = [-0.04; 0.04; 0];
    t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400];
    y = dae("stiff", [x0, xd0], 0, t, rtol, atol, 'chemres', 'addap');
    y = dae("stiff", [x0, xd0], 0, t, rtol, atol, 'chemres', 'chemjac', 'addap'); // With jacobian

Voir aussi

  • dae_root — differential algebraic equation solver with roots finding
  • ode — solveur d'équations différentielles ordinaires
  • daeoptions — set options for dae solver
  • call — Fortran or C user routines call
  • link — dynamic linker
  • external — Objet Scilab, fonction externe ou routine

History

VersionDescription
2024.1.0 dassl, dasrt and daskr deviennent des fonctions internes.
2025.0.0 impl devient une fonction interne.
Report an issue
<< bvode Equations différentielles dae_root >>
Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors 		Last updated:
Thu Oct 24 11:15:57 CEST 2024