dae

Arguments

y0: a column vector or a matrix. It may be equal to x0 or [x0, xdot0]. Where x0 is the state value at initial time t0 and xdot0 is the initial state derivative value or an estimation of it (see below).
t0: a real number, the initial time.
t: a real scalar or vector. Gives instants for which you want the solution. Note that you can get solution at each dae's step point by setting %DAEOPTIONS(2)=1 .
rtol: a real scalar or a column vector of same size as x0, the relative error tolerance of solution. If rtol is a vector the tolerances are specified for each component of the state.
atol: a real scalar or a column vector of same size as x0, the absolute error tolerance of solution. If atol is a vector the tolerances are specified for each component of the state.
res: an external function, computes the value of g(t, y, ydot). It may be a Scilab function, list or string. The syntax differs depending on the solver used. See residual description section for more details.
jac: an external function, computes the Jacobian of the function g(t, y, ydot). It may be a Scilab function, list or string. The syntax differs depending on the solver used. See jacobian description section for more details.
surface: an external (function, list or string), computes the value of the column vector surface(t,x) with ng components. Each component defines a surface. Used ONLY with dasrt ("root") and daskr ("root2") solvers. For more details, see surface description section.
adda: an external (function, list or string), computes p = p + a with a = a(t,y). Used ONLY with "stiff" and "adams" solver. See adda description section for more details.
psol: external (function, list or string). Used ONLY with "root2" (daskr) solver. Solves a linear system P*x = b, with P being the factored preconditioner that routine pjac computed beforehand and stored in wp and iwp. See psol description section for more details.
pjac: external (function, list or string). Used ONLY with "root2" (daskr) solver. Computes the value of dg/dy + cj*dg/dydot for a given value of parameter cj and LU-factorizes it in two arrays, real and integer. See pjac description section for more details.
y: a real matrix. If %DAEOPTIONS(2)=1 , each column is the vector [t;x(t);xdot(t)] where t is time index for which the solution has been computed. Else y is the vector [x(t);xdot(t)].
rd: a vector with two entries [times num] where times is the value of the time at which the surface is crossed, num is the number of the crossed surface
hd: a real vector, as an output it stores the dae context. It can be used as an input argument to resume integration (hot restart).

Description

The dae function solves the differential algebraic equation and returns the evolution of y a given time points

g(t, x, xdot) = 0
x(t0) = x0 and xdot(t0) = xdot0

If xdot0 is not given in the y0 argument, the dae function tries to compute it solving g(t,x0,xdot0)=0.

If xdot0 is given in the y0 argument it may be either a compatible derivative satisfying g(t,x0,xdot0)=0 or an approximate value. In the latter case %DAEOPTIONS(7) must be set to 1.

The solvers

The type of problem solved and the method used depend on the value of the first optional argument type which can be one of the following strings:

<not given>:: the dassl solver.
"root":: the dasrt solver. See help on dae_root for more details.
"root2":: the daskr solver. See help on dae_root for more details.
"adams":: This is for nonstiff problems. lsodi solver of package ODEPACK is called and it uses the Adams method.
"stiff":: This is for stiff problems. lsodi solver of package ODEPACK is called and it uses the BDF method.

Residual function

The input argument res is the right hand side usually called "residual" of the DAE. It is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list. The function syntax differs depending on used solver when res is the character string.

a Scilab function

In this case, the syntax must be

[r, ires] = res(t, y, ydot)

where res must return the residue and error flag ires.

ires = 0 if res succeeds to compute r.

ires = -1 if residue is locally not defined for g(t, x, xdot).

ires =-2 if parameters are out of admissible range.

If adams or stiff solver is used, this function must return r = g(t,y)-A(t,y)*ydot

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(res, p1, p2, ...)

where the syntax of the function res is now

r = res(t, y, ydot, p1, p2, ...)

res still returns the residual value as a function of (t, x, xdot, x1, x2, ...), and p1, p2,... are function parameters.

a character string

It must refer to the name of a C or Fortran routine. In function of solver, the syntax is different. Assuming that <r_name> is the given name,

If dassl, dasrt ("root") or daskr ("root2") solver is used, res may be

The Fortran calling sequence must be

subroutine <r_name>(t, x, xdot, res, ires, rpar, ipar)
double precision t, x(*), xdot(*), res(*), rpar(*)
integer ires, ipar(*)

The C syntax must be

void <r_name>(double *t, double *x, double *xdot, double *res, int *ires, double *rpar, int *ipar)

where

t is the current time value
x the state array
xdot the array of state derivatives
res the array of residuals
ires the execution indicator
rpar is the array of floating point parameter values, needed but cannot be set by the dae function
ipar is the array of floating integer parameter values, needed but cannot be set by the dae function

If adams or stiff solvers is used, res may be

The Fortran calling sequence must be

subroutine <r_name>(neq, t, x, xdot, res, ires)
double precision t, x(*), xdot(*), res(*)
integer neq, ipar(*)

The C syntax must be

void <r_name>(int *neq, double *t, double *x, double *xdot, double *res, int *ires)

where

neq is the number of equations in the system
t is the current time value
x the state array
xdot the array of state derivatives
res the array of residuals
ires the execution indicator

Jacobian function

The input argument jac computes the jacobian. As res, jac is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list. The function syntax differs depending on used solver.

If dassl, dasrt ("root") or daskr ("root2") solver is used, jac computes the value of dg/dx + cj * dg/dxdot for a given value of parameter cj. It may be

a Scilab function

In this case, the syntax must be

j = jac(t, y, ydot, cj)

where jac function must return

j = dg(t, x, xdot)/dy + cj * dg(t, x, xdot)/dxdot

where cj is a real scalar.

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(jac, p1, p2, ...)

where the syntax of the function jac is now

r = jac(t, x, xdot, cj, p1, p2, ...)

jac still returns dg/dx+cj*dg/dxdot as a function of (t,x,xdot,cj,p1,p2,...).

a character string

It must refer to the name of a C or Fortran routine. Assuming that <j_name> is the given name,

The Fortran calling sequence must be

subroutine <j_name>(t, x, xdot, r, cj, ires, rpar, ipar)
double precision t, x(*), xdot(*), r(*), cj, rpar(*)
integer ires, ipar(*)

The C syntax must be

void <j_name>(double *t, double *x, double
*xdot, double *r, double *cj, int *ires, double *rpar, int *ipar)

where t, x, xdot, ires, rpar, ipar have similar definition as above, r is the results array

For adams or stiff solver, jac may be

a Scilab function

In this case, the syntax must be

j = jac(t, y, ydot)

where jac function must return the Jacobian of r = g(t,y)-A(t,y)*ydot with respect to y.

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(jac, p1, p2, ...)

where the syntax of the function jac is now

r = jac(t, y, ydot, p1, p2, ...)

a character string

It must refer to the name of a C or Fortran routine. Assuming that <j_name> is the given name,

The Fortran calling sequence must be

subroutine <j_name>(neq, t, x, xdot, ml, mu, j, nrpd)
double precision t, x(*), xdot(*), j(*)
integer neq, ml, mu, nrpd

The C syntax must be

void <j_name>(int *neq, double *t, double *x, double *xdot, int *ml, int *mu, double *j, int *nrpd)

Surface function

The input argument surface, used ONLY with dassl, dasrt ("root") or daskr ("root2") solver, computes the value of the column vector surface(t,x) with ng components. Each component defines a surface. As res, is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list.

a Scilab function

Its syntax must be

r=surface(t,x)

this function must return a vector with ng elements.

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(surface,p1,p2,...)

where the syntax of the function surface is now

r = surface(t,x,p1,p2,...)

a character string

it must refer to the name of a C or Fortran routine. Assuming that <s_name> is the given name,

The Fortran calling sequence must be

subroutine <s_name>(nx, t, x, ng, r, rpar, ipar)
double precision t, x(*), r(*), rpar(*)
integer nx, ng,ipar(*)

The C syntax must be

void <s_name>(int *nx, double *t, double *x, int *ng, double *r, double *rpar, int *ipar)

where t, x, rpar, ipar have similar definition as above, ng is the number of surfaces, nx the dimension of the state and r is the results array.

adda function

The input argument adda, used ONLY with adams and stiff solvers, computes r = A(t,y) + p where p is a matrix to be added to A(t,y). As res, is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list.

a Scilab function

Its syntax must be

r=adda(t, y, p)

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(adda,p1,p2,...)

where the syntax of the function adda is now

adda(t,x,p1,p2,...)

a character string

it must refer to the name of a C or Fortran routine. Assuming that <a_name> is the given name,

The Fortran calling sequence must be

subroutine <a_name>(nx, t, x, ml, mu, p, nrpd)
double precision t, x(*), p(*)
integer nx, ml, mu, nrpd

The C syntax must be

void <a_name>(int *nx, double *t, double *x, int *ml, int *mu, double *p, int *nrpd)

In most cases you have not to refer ml, mu and nrpd.

psol function

The input argument psol, used ONLY with daskr solver, solves a linear system P*x = b, with P being the factored preconditioner that routine pjac computed beforehand and stored in wp and iwp. As res, is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list.

a Scilab function

Its syntax must be

[r, ier] = psol(wp, iwp, b)

and must return the solution of the system in r and an error flag ier.

a list

It must be as follows:

list(psol,p1,p2,...)

where the syntax of the function psol is now

psol(wp, iwp, b, x1, x2, ...)

a character string

it must refer to the name of a C or Fortran subroutine linked with Scilab,

The Fortran calling sequence must be

subroutine psol (neq, t, y, ydot, savr, wk, cj, wght, wp, iwp, b, eplin, ier, rpar, ipar)
double precision t,y(*), ydot(*), savr(*), wk(*), cj, wght(*), wp(*), b(*), eplin, rpar(*)
integer neq, iwp(*), ier, ipar(*)

The C syntax must be

void psol (int*neq, double*t, double*y, double*ydot, double*savr, double*wk, double*cj, double*wght, double*wp, int*iwp, double*b, double*eplin, int*ier, double*rpar, int*ipar)

where the arrays wp and iwp contain matrix elements of LU-factored preconditioner P, wp being the values and iwp the pivots used in the factorization.

pjac function

The input argument pjac, used ONLY with daskr solver, computes the value of dg/dy + cj*dg/dydot for a given value of parameter cj and LU-factorizes it in two arrays, real and integer. As res, is an external i.e. a function with specifed syntax, or the name a Fortran subroutine or a C function (character string) with specified syntax or a list.

a Scilab function

Its syntax must be

[wp, iwp, ires] = pjac(neq, t, y, ydot, h, cj, rewt, savr)

and in return, the arrays wp and iwp must contain all factored preconditioner information.

a list

It must be as follows:

list(pjac, x1, x2,...)

where the syntax of the function surface is now

pjac(neq, t, y, ydot, h, cj, rewt, savr, x1, x2,...)

pjac still returns factorized dg/dy + cj*dg/dydot as a function of (neq, t, y, ydot, h, cj, rewt, savr, x1, x2, ...).

a character string

it must refer to the name of a C or Fortran subroutine linked with Scilab

The Fortran calling sequence must be

subroutine pjac (res, ires, neq, t, y, ydot, rewt, savr, wk, h, cj, wp, iwp, ier, rpar, ipar)
double precision res(*), t, y(*), ydot(*), rewt(*), savr(*),  wk(*), h, cj, wp(*), rpar(*)
integer ires, neq, iwp(*), ier, ipar(*)

The C syntax must be

void pjac (double*res, int*ires, int*neq, double*t, double*y, double*ydot, double*rewt, double*savr, double*wk, double*h, double*cj, double*wp, int*iwp, int*ier, double*rpar, int*ipar)

In most cases you have not to refer ml, mu and nrpd.

Examples

Example #1: use dassl solver

// Example with Scilab code
//--------------------------------------------------
function [r, ires]=chemres(t, y, yd)
    r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1);
    r(2) =  0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2);
    r(3) =       y(1) +     y(2)      + y(3)-1;
    ires =  0;
endfunction

function pd=chemjac(x, y, yd, cj)
    pd = [-0.04-cj , 1d4*y(3)               , 1d4*y(2);
           0.04    ,-1d4*y(3)-2*3d7*y(2)-cj ,-1d4*y(2);
           1       , 1                      , 1       ]
endfunction

x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400, 4000, 40000, 4d5, 4d6, 4d7, 4d8, 4d9, 4d10];

y = dae([x0, xd0], 0, t, chemres); // Returns requested observation time points

%DAEOPTIONS = list([], 1, [], [], [], 0, 0); // Ask  dae mesh points to be returned
y = dae([x0, xd0], 0, 4d10, chemres); // Without jacobian
y = dae([x0, xd0], 0, 4d10, chemres, chemjac); // With jacobian

Example #2: use dasrt solver with "root"

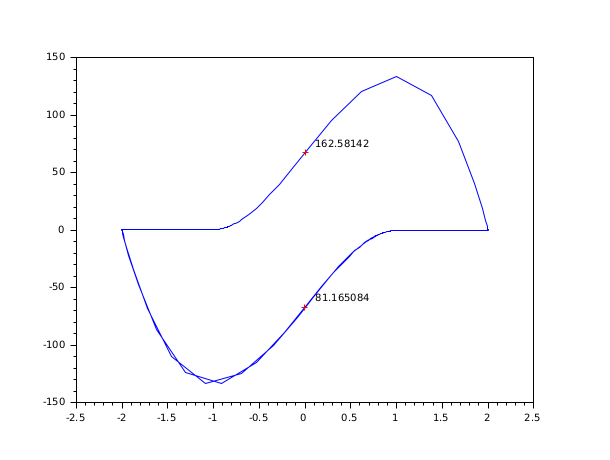
// Example with C code (C compiler needed)
//--------------------------------------------------
bOK = haveacompiler();
if bOK <> %t
    [btn] = messagebox(["You need a C compiler for this example."; "Execution of this example is canceled."], "Software problem", 'info');
    return
end

//-1- Create the C codes in TMPDIR - Vanderpol equation, implicit form
code = ['#include <math.h>'
      'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)'
      '{res[0] = yd[0] - y[1];'
      ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}'
      ' '
      'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)'
      '{pd[0] = *cj - 0.0;'
      ' pd[1] =     - (-200.0*y[0]*y[1] - 1.0);'
      ' pd[2] =     - 1.0;'
      ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}'
      ' '
      'void gr22(int *neq, double *t, double *y, int *ng, double *groot, double *rpar, int *ipar)'
      '{ groot[0] = y[0];}']
previous_dir = pwd();
cd TMPDIR;
mputl(code, 't22.c')

//-2- Compile and load them
ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce');
exec('t22loader.sce')

//-3- Run
rtol = [1.d-6; 1.d-6];
atol = [1.d-6; 1.d-4];
t0 = 0; t = [20:20:200];
y0 = [2; 0]; y0d = [0; -2];
ng = 1;

// Simple simulation
t = 0:0.003:300;
yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22');
clf(); plot(yy(1, :), yy(2, :))
// Find first point where yy(1) = 0
[yy, nn, hotd] = dae("root", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22');
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));

// Hot restart for next point
t01 = nn(1);
[pp, qq] = size(yy);
y01 = yy(2:3, qq); y0d1 = yy(3:4, qq);
[yy, nn, hotd] = dae("root", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', hotd);
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));
cd(previous_dir);

Example #3: use daskr solver with "root2", using default 'psol' and 'pjac' routines

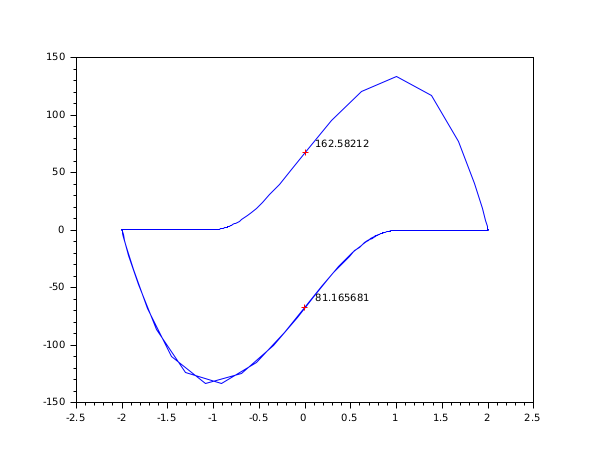
// Example with C code (C compiler needed)
//--------------------------------------------------
bOK = haveacompiler();
if bOK <> %t
    [btn] = messagebox(["You need a C compiler for this example."; "Execution of this example is canceled."], "Software problem", 'info');
    return
end

//-1- Create the C codes in TMPDIR - Vanderpol equation, implicit form
code = ['#include <math.h>'
      'void res22(double *t, double *y, double *yd, double *res, int *ires, double *rpar, int *ipar)'
      '{res[0] = yd[0] - y[1];'
      ' res[1] = yd[1] - (100.0*(1.0 - y[0]*y[0])*y[1] - y[0]);}'
      ' '
      'void jac22(double *t, double *y, double *yd, double *pd, double *cj, double *rpar, int *ipar)'
      '{pd[0] = *cj - 0.0;'
      ' pd[1] =     - (-200.0*y[0]*y[1] - 1.0);'
      ' pd[2] =     - 1.0;'
      ' pd[3] = *cj - (100.0*(1.0 - y[0]*y[0]));}'
      ' '
      'void gr22(int *neq, double *t, double *y, double *yd, int *ng, double *groot, double *rpar, int *ipar)'
      '{ groot[0] = y[0];}']
previous_dir = pwd();
cd TMPDIR;
mputl(code, 't22.c')

//-2- Compile and load them
ilib_for_link(['res22' 'jac22' 'gr22'], 't22.c', [], 'c', [], 't22loader.sce');
exec('t22loader.sce')

//-3- Run
rtol = [1.d-6; 1.d-6];
atol = [1.d-6; 1.d-4];
t0 = 0; t = [20:20:200];
y0 = [2; 0]; y0d = [0; -2];
ng = 1;

// Simple simulation
t = 0:0.003:300;
yy = dae([y0, y0d], t0, t, atol, rtol, 'res22', 'jac22');
clf(); plot(yy(1, :), yy(2, :))
// Find first point where yy(1) = 0
%DAEOPTIONS = list([] , 0, [], [], [], 0, [], 1, [], 0, 1, [], [], 1);
[yy, nn, hotd] = dae("root2", [y0, y0d], t0, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1');
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));

// Hot restart for next point
t01 = nn(1);
[pp, qq] = size(yy);
y01 = yy(2:3, qq); y0d1 = yy(3:4, qq);
[yy, nn, hotd] = dae("root2", [y01, y0d1], t01, 300, atol, rtol, 'res22', 'jac22', ng, 'gr22', 'psol1', 'pjac1', hotd);
plot(yy(1, 1), yy(2, 1), 'r+')
xstring(yy(1, 1)+0.1, yy(2, 1), string(nn(1)));
cd(previous_dir);

Example #4: use stiff solver

// Example with Scilab code
//--------------------------------------------------
function [r, ires]=chemres(t, y, yd)
r(1) = -0.04*y(1) + 1d4*y(2)*y(3) - yd(1);
r(2) =  0.04*y(1) - 1d4*y(2)*y(3) - 3d7*y(2)*y(2) - yd(2);
r(3) =       y(1) +     y(2)      + y(3)-1;
ires =  0;
endfunction

function j=chemjac(t, y, yd)
j = [-0.04 , 1d4*y(3)               , 1d4*y(2);
0.04    ,-1d4*y(3)-2*3d7*y(2) ,-1d4*y(2);
1       , 1                      , 1       ]
endfunction

function p=addap(t, y, p)
    p(1,1) = p(1,1) + 1;
    p(2,2) = p(2,2) + 1;
endfunction

x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400];

y = dae("stiff", [x0, xd0], 0, t, chemres, addap);
y = dae("stiff", [x0, xd0], 0, t, chemres, chemjac, addap); // With jacobian

Example #5: use stiff solver with a compiler

code = ['#include <math.h>'
  'void chemres(int *neq, double *t, double *y, double *s, double *res, int *ires, double *rpar, int *ipar)'
  '{res[0] = -0.040*y[0] + 1.0e4*y[1]*y[2] - s[0];'
  ' res[1] = 0.040*y[0] - 1.0e4*y[1]*y[2] - 3.0e7*y[1]*y[1] - s[1];'
  'res[2] = y[0] + y[1] + y[2] - 1.0;}'
  ' '
  'void chemjac(int *neq, double *t, double *y, double *s, double *ml, double *mu, double *p, int *nrowp)'
  '{p[0] = -0.04;'
  ' p[1] = 0.040;'
  ' p[2] = 1.0;'
  'p[3] = 1.0e4*y[2];'
  ' p[4] = -1.0e4*y[2] - 6.0e7*y[1];'
  ' p[5] = 1.0;'
  'p[6] = 1.0e4*y[1];'
 ' p[7] = -1.0e4*y[1];'
 ' p[8] = 1.0;}'
  ' '
  'void addap(int *neq, double *t, double *y, double *ml, double *mu, double *p, int *nrowp)'
  '{ p[0] = p[0] + 1.0;'
  'p[4] = p[4] + 1.0;'
  '}']

mputl(code, fullfile(TMPDIR, 'mydae.c'))

//-2- Compile and load them
cd TMPDIR
ilib_for_link(['chemres' 'chemjac' 'addap'], 'mydae.c', [], 'c', [], 'loader.sce');
exec('loader.sce')

//-3- Run
rtol = [1d-6; 1d-6; 1d-6];
atol = [1d-6; 1d-6; 1d-4];
t0 = 0;
x0 = [1; 0; 0];
xd0 = [-0.04; 0.04; 0];
t = [1.d-5:0.02:.4, 0.41:.1:4, 40, 400];
y = dae("stiff", [x0, xd0], 0, t, rtol, atol, 'chemres', 'addap');
y = dae("stiff", [x0, xd0], 0, t, rtol, atol, 'chemres', 'chemjac', 'addap'); // With jacobian

History

Versão	Descrição
2024.1.0	dassl, dasrt and daskr become internal.
2025.0.0	impl becomes internal.

Report an issue
<< bvode	Equações Diferenciais	dae_root >>

Syntax

Arguments

Description

The solvers

Residual function

Jacobian function

Surface function

adda function

psol function

pjac function

Examples

See also

History