splin

引数

x

単調増加する (列または行) ベクトル (x は2つ以上の要素を有する 必要があります)

y

xと同じ大きさのベクトル

spline_type

(オプション) 計算するスプラインの種類を選択する文字列

der

(オプション) 2つの要素を有するベクトルで, (spline_type="clamped"の場合に使用される)端点の微係数を有します

d

xと同じ形式のベクトル (di は, xi)におけるスプラインの微係数です.

説明

この関数は, 点(xi,yi)を補間する,すなわち, i=1,..,nについてs(xi)=yi となる 3次スプラインまたはサブスプラインs を計算します. 得られるスプライン sは, (x,y,d)により完全に定義されます. ただし,dはxiにおける 微係数のベクトルです: s'(xi)=di (これは エルミート形式と呼ばれます). いつくかの点におけるスプラインの評価はinterp 関数により行われます. 適当なspline_typeパラメータを選択することにより, いくつかの種類のスプラインを計算することができます:

"not_a_knot"

これはデフォルトで, 3次スプラインが以下の条件 (n個の点 x1,...,xnを考慮)により計算されます:

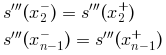
"clamped"

この場合,3次スプラインは端点における微係数 を用いて計算されます.この微係数は最後の引数der で指定されます:

s'(x1) = der(1)

s'(xn) = der(2)

"natural"

3次スプラインは次の条件により計算されます:

s''(x1) = 0

s''(xn) = 0

"periodic"

周期的3次スプラインは次の条件により計算されます (yはy1=ynを確認する必要があります):

s'(x1) = s'(xn)

s''(x1) = s''(xn)

"monotone"

この場合,サブスプライン (s は 1回のみ連続的に微分可能)は,sが 各区間で単調となるようなdi に関するローカルなスキームにより計算されます:

• If y(i) ≤ y(i+1), s is increasing on [x(i), x(i+1)].
• If y(i) ≥ y(i+1), s is increasing on [x(i), x(i+1)].

"fast"

この場合, サブスプラインもdi に関する簡単でローカルなスキームにより計算されます: d(i) は (x(i-1),y(i-1)), (x(i),y(i)),(x(i+1),y(i+1)) の多項式補間の x(i) における微係数です. ただし,端点を除きます (d1 は最も左の3点から, dn は最も右の3点から計算されます).

"fast_periodic"

前のオプションと同じですが,基本となる関数の周期性に 基づき d1 = s'(x1) = dn = s'(xn)に関する 中心化式も使用します (yはy1=ynも 満たす必要があります).

注意

精度の観点からは,端点の微係数が既知の場合, 基本的にclamped型を使用してください. そうでない場合は,not_a_knot型を使用して ください. しかし,基本的な近似関数に周期性がある場合には, periodic型を使用してください. 良い近似を行うことで,これらの種類のスプラインは,誤差の漸近特性 としてO(h^4)を得ることができます. 基本関数の2階微分が0でない限り, naturalを使用しないでください.

monotone, fast (または fast_periodic) 型は,振動を抑制する といったいくつかのケースでは有用です (これらの種類のサブスプラインはO(h^3)の 誤差漸近特性を有します).

n=2の(そしてspline_type が clampedではない) 場合, 線形補間が使用されます. n=3 で spline_type が not_a_knotの場合, fast サブスプライン型が実際に計算されます.

例

// 例 1
deff("y=runge(x)","y=1 ./(1 + x.^2)")
a = -5; b = 5; n = 11; m = 400;
x = linspace(a, b, n)';
y = runge(x);
d = splin(x, y);
xx = linspace(a, b, m)';
yyi = interp(xx, x, y, d);
yye = runge(xx);
clf()
plot2d(xx, [yyi yye], style=[2 5], leg="interpolation spline@exact function")
plot2d(x, y, -9)
xtitle("interpolation of the Runge function")

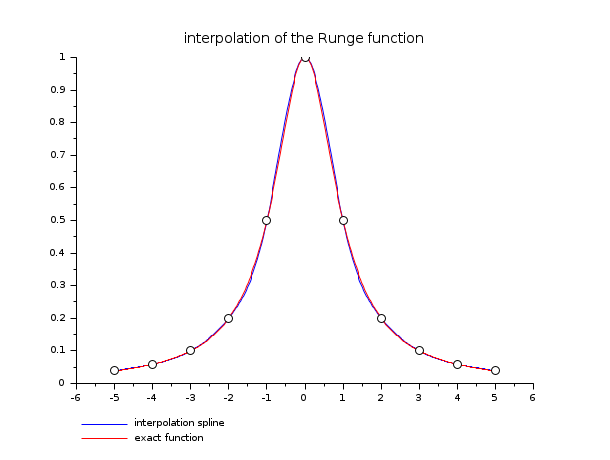
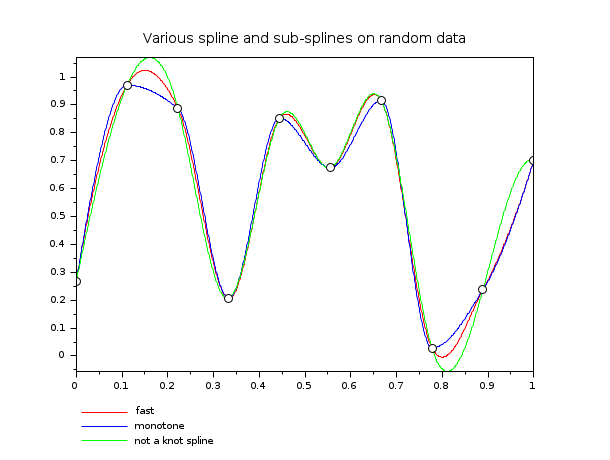
// 例 2 : ランダムなデータで異なるスプラインの動作を示す
a = 0; b = 1;        // 補間の間隔
n = 10;              // 補間点のnb
m = 800;             // 評価を行う離散点
x = linspace(a,b,n)'; // 補間点の横座標
y = rand(x);          // 補間点の縦座標
xx = linspace(a,b,m)';
yk = interp(xx, x, y, splin(x,y,"not_a_knot"));
yf = interp(xx, x, y, splin(x,y,"fast"));
ym = interp(xx, x, y, splin(x,y,"monotone"));
clf()
plot2d(xx, [yf ym yk], style=[5 2 3], strf="121", ...
       leg="fast@monotone@not a knot spline")
plot2d(x,y,-9, strf="000")  // to show interpolation points
xtitle("Various spline and sub-splines on random data")
show_window()

参照

• interp — 3次スプライン評価関数
• lsq_splin — 重み付き最小二乗三次スプラインフィッティング