damp
固有周波数およびダンピング乗数.
呼び出し手順
[wn,z] = damp(sys) [wn,z] = damp(P [,dt]) [wn,z] = damp(R [,dt])
パラメータ
- sys
線形ダイナミクスシステム (syslin参照).
- P
多項式配列.
- P
実数または複素数の浮動小数点数の配列.
- dt
非負のスカラー, デフォルト値は 0.
- wn
昇順の浮動小数点数のベクトル:固有周波数 [rad/s].
- z
浮動小数点数のベクトル: ダンピング乗数.
説明
複素極を有する分母の二次連続時間伝達関数は
s^2+2*z*wn*s+wn^2のように記述できます。
ただし,z はダンピング乗数, wn
は固有周波数です.
sys が連続時間系の場合,
[wn,z] = damp(sys) は
線形ダイナミクスシステムsysの極の
固有周波数 ωn (rad/s)をwn に
ダンピング係数 ξをzに
返します.配列 wn と
zは周波数に関して昇順となります.
sys が離散時間系の場合,
[wn,z] = damp(sys) は
sysの連続時間系で等価な極の
固有周波数 ωn (rad/s)をwn に
ダンピング乗数 ξをzに
返します.配列 wn と
zは周波数に関して昇順となります.
[wn,z] = damp(P) は,
配列 Pに保存された多項式の根の集合の
固有周波数 ωn (rad/s) をwn,
ダンピング乗数 ξをzに返します.
dt が指定され, 0でない場合,
その根はまず連続時間系の等価な根に変換されます.
配列 wn およびz は
周波数に関して昇順となります.
[wn,z] = damp(R) は,
配列Rに保存された根の集合の
固有周波数 ωn (rad/s)をwn に
ダンピング乗数 ξをzに
返します.
dt が指定され, 0でない場合,
その根はまず連続時間系の等価な根に変換されます.
配列 wn(i) およびz(i) は
それぞれR(i)の固有周波数およびダンピング乗数と
なります.
例
s=%s; num=22801+4406.18*s+382.37*s^2+21.02*s^3+s^4; den=22952.25+4117.77*s+490.63*s^2+33.06*s^3+s^4 h=syslin('c',num/den); [wn,z] = damp(h)
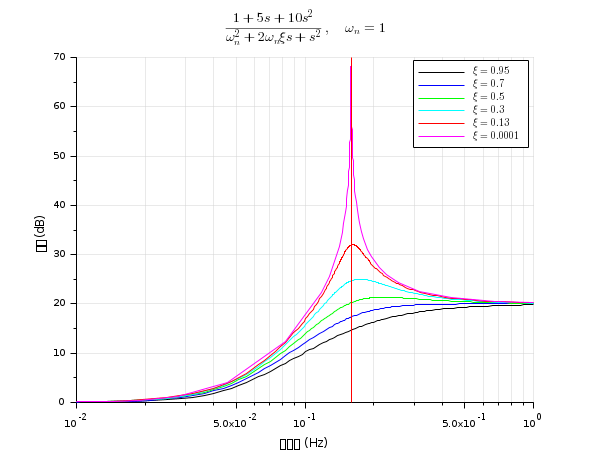
以下の例は二次系の周波数応答に関するダンピング乗数の感度を 示すものです.
s=%s; wn=1; clf(); Z=[0.95 0.7 0.5 0.3 0.13 0.0001]; for k=1:size(Z,'*') z=Z(k) H=syslin('c',1+5*s+10*s^2,s^2+2*z*wn*s+wn^2); gainplot(H,0.01,1) p=gce();p=p.children; p.foreground=k; end title("$\frac{1+5 s+10 s^2}{\omega_n^2+2\omega_n\xi s+s^2}, \quad \omega_n=1$") legend('$\xi='+string(Z)+'$') plot(wn/(2*%pi)*[1 1],[0 70],'r') // 固有周波数
根の集合の固有周波数とダンピング比を計算します:
[wn,z] = damp((1:5)+%i)
履歴
| バージョン | 記述 |
| 6.0 | handling zpk representation |
| Report an issue | ||
| << csim | Time Domain | dsimul >> |