delip
полный и неполный эллиптический интеграл первого рода
Синтаксис
r = delip(x, ck)
Аргументы
- x
вещественный вектор/матрица с неотрицательными элементами.
- ck
вещественное число между -1 и 1
- r
вещественное или комплексное число (или вектор/матрица) того же размера, что и
x
Описание
Эллиптический интеграл первого рода с параметром ck
определяется как:
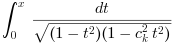
Где x - вещественное положительное число,
ck - лежит на интервале [-1 1].
Если x меньше 1, то результат вещественный.
Вектор/матрица r
вычисляется для каждого элемента x.
Примеры
Смотрите также
| Report an issue | ||
| << dawson | Special Functions | dlgamma >> |