interp
cubic spline evaluation function
Syntax
[yp, yp1, yp2, yp3] = interp(xp, x, y, d) [yp, yp1, yp2, yp3] = interp(xp, x, y, d, out_mode)
Arguments
- x,y
real vectors of same size
n: Coordinates of data points on which the interpolation and the related cubic spline (calleds(X)in the following) or sub-spline function is based and built.- d
real vector of size(x): The derivative s'(x). Most often, s'(x) will be priorly estimated through the function splin(x, y,..)
- out_mode
(optional) string defining
s(X)forXoutside [x1, xn]. Possible values: "by_zero" | "by_nan" | "C0" | "natural" | "linear" | "periodic"- xp
real vector or matrix: abscissae at which
Yis unknown and must be estimated withs(xp)- yp
vector or matrix of size(xp):
yp(i) = s(xp(i))oryp(i,j) = s(xp(i,j))- yp1, yp2, yp3
vectors (or matrices) of size(x): elementwise evaluation of the derivatives
s'(xp),s''(xp)ands'''(xp).
Description
The cubic spline function s(X) interpolating the (x,y)
set of given points is a continuous and derivable piece-wise function defined over
[x1, xn]. It consists of a set of cubic polynomials, each one
pk(X) being defined on [xk, xk+1]
and connected in values and slopes to both its neighbours. Thus, we can state that for each
X ∈ [xk, xk+1],
s(X) = pk(X), such that
s(xi) = yi, and
s'(xi) = di.
Then, interp() evaluates s(X) (and s'(X), s''(X), s'''(X)
if needed) at xp(i), such that
| ypi = s(xpi) or ypij = s(xpij) |
| yp1i = s'(xpi) or yp1ij = s'(xpij) |
| yp2i = s''(xpi) or yp2ij = s''(xpij) |
| yp3i = s'''(xpi) or yp3ij = s'''(xpij) |
The out_mode parameter set the evaluation rule
for extrapolation, i.e. for xp(i) outside [x1, xn] :
- "by_zero"
an extrapolation by zero is done
- "by_nan"
extrapolation by Nan (%nan)
- "C0"
the extrapolation is defined as follows :
xpi < x1 ⇒ ypi = y1 xpi > xn ⇒ ypi = yn - "natural"
the extrapolation is defined as follows (pi(x) being the polynomial defining
s(X)on [xi, xi+1]):xpi < x1 ⇒ ypi = p1(xpi) xpi > xn ⇒ ypi = pn-1(xpi) - "linear"
the extrapolation is defined as follows :
xpi < x1 ⇒ ypi = y1 + d1.(xpi - x1) xpi > xn ⇒ ypi = yn + dn.(xpi - xn) - "periodic"
s(X)is extended by periodicity:ypi = s( x1 + (xpi - x1) modulo (xn-x1) )
Examples
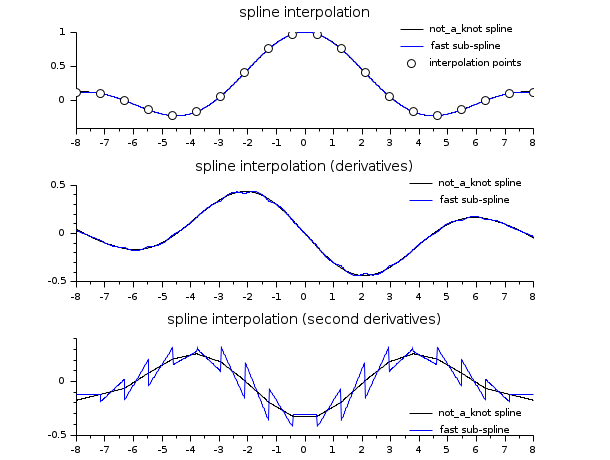
// see the examples of splin and lsq_splin // an example showing C2 and C1 continuity of spline and subspline a = -8; b = 8; x = linspace(a,b,20)'; y = sinc(x); dk = splin(x,y); // not_a_knot df = splin(x,y, "fast"); xx = linspace(a,b,800)'; [yyk, yy1k, yy2k] = interp(xx, x, y, dk); [yyf, yy1f, yy2f] = interp(xx, x, y, df); clf() subplot(3,1,1) plot2d(xx, [yyk yyf]) plot2d(x, y, style=-9) legends(["not_a_knot spline","fast sub-spline","interpolation points"],... [1 2 -9], "ur",%f) xtitle("spline interpolation") subplot(3,1,2) plot2d(xx, [yy1k yy1f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "ur",%f) xtitle("spline interpolation (derivatives)") subplot(3,1,3) plot2d(xx, [yy2k yy2f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "lr",%f) xtitle("spline interpolation (second derivatives)")
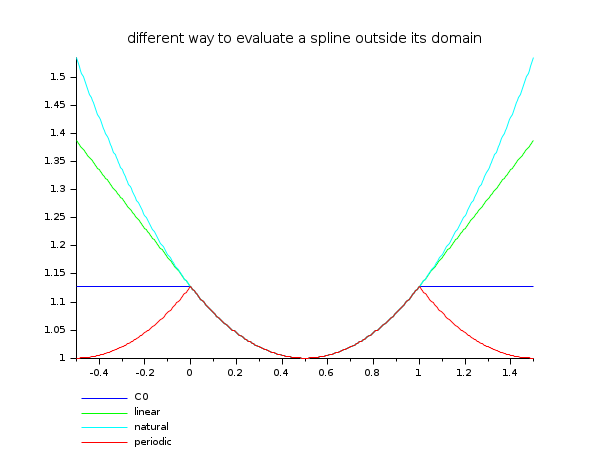
// here is an example showing the different extrapolation possibilities x = linspace(0,1,11)'; y = cosh(x-0.5); d = splin(x,y); xx = linspace(-0.5,1.5,401)'; yy0 = interp(xx,x,y,d,"C0"); yy1 = interp(xx,x,y,d,"linear"); yy2 = interp(xx,x,y,d,"natural"); yy3 = interp(xx,x,y,d,"periodic"); clf() plot2d(xx,[yy0 yy1 yy2 yy3],style=2:5,frameflag=2,leg="C0@linear@natural@periodic") xtitle(" different way to evaluate a spline outside its domain")
| Report an issue | ||
| << eval_cshep2d | Interpolation | interp1 >> |