interp
função de avaliação de spline cúbico
Seqüência de Chamamento
[yp, yp1, yp2, yp3] = interp(xp, x, y, d) [yp, yp1, yp2, yp3] = interp(xp, x, y, d, out_mode)
Parâmetros
- xp
vetor ou matriz de reais
- x,y,d
vetores de reais de mesmo tamanho definindo uma função de spline cúbico ou sub-spline (chamado
sa partir daqui)- out_mode
(opcional) string definido a avaliação de
sfora do intervalo [x1, xn].- yp
vetor ou matriz de mesmo tamanho que
xp, avaliação elemento a elemento desemxp(yp(i)=s(xp(i) ou yp(i,j)=s(xp(i,j))- yp1, yp2, yp3
vetores (ou matrizes) de mesmo tamanho que
xp, avaliação elemento a elemento das derivadas sucessivas desemxp
Descrição
Dados três vetores (x,y,d) ddefinindo uma função
de spline cúbico ou sup-spline (ver splin)
com
s(xi) = yi, e
s'(xi) = di
esta função avalia
s (e s', s'', s''' se necessário) em
xp(i) :
| ypi = s(xpi) ou ypij = s(xpij) |
| yp1i = s'(xpi) ou yp1ij = s'(xpij) |
| yp2i = s''(xpi) ou yp2ij = s''(xpij) |
| yp3i = s'''(xpi) ou yp3ij = s'''(xpij) |
O parâmetro out_mode ajusta a regra de avaliação
para extrapolação, i.e., para xp(i) fora de
[x1, xn] :
- "by_zero"
uma extrapolação por zero é feita
- "by_nan"
extrapolação por NaN
- "C0"
a extrapolação é definida como segue :
xpi < x1 ⇒ ypi = y1 xpi > xn ⇒ ypi = yn - "natural"
a extrapolação é definida como segue (pi(x) sendo o polinômio que define
sem [xi, xi+1]) :xpi < x1 ⇒ ypi = p1(xpi) xpi > xn ⇒ ypi = pn-1(xpi) - "linear"
a extrapolação é definida como segue :
xpi < x1 ⇒ ypi = y1 + d1.(xpi - x1) xpi > xn ⇒ ypi = yn + dn.(xpi - xn) - "periodic"
sé estendido por periodicidade :ypi = s( x1 + (xpi - x1) modulo (xn-x1) )
Exemplos
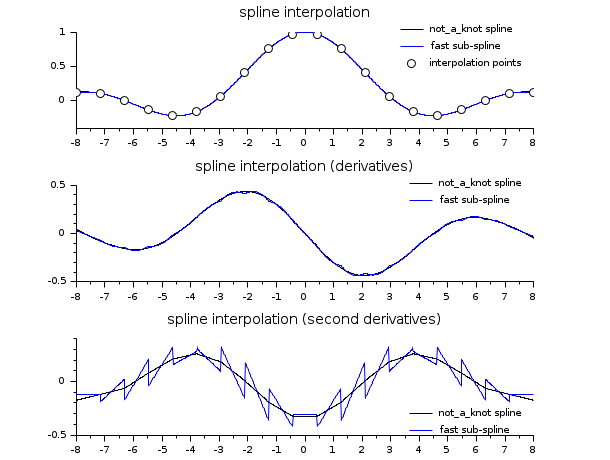
// veja os exemplos de splin e lsq_splin // um exemplo exibindo as continuidades C2 e C1 de um spline e um sub-spline a = -8; b = 8; x = linspace(a,b,20)'; y = sinc(x); dk = splin(x,y); // not_a_knot df = splin(x,y, "fast"); xx = linspace(a,b,800)'; [yyk, yy1k, yy2k] = interp(xx, x, y, dk); [yyf, yy1f, yy2f] = interp(xx, x, y, df); clf() subplot(3,1,1) plot2d(xx, [yyk yyf]) plot2d(x, y, style=-9) legends(["spline não é um nó","sub-spline rápido","pontos de interpolação"],... [1 2 -9], "ur",%f) xtitle("interpolação por spline") subplot(3,1,2) plot2d(xx, [yy1k yy1f]) legends(["spline não é um nó","sub-spline rápido"], [1 2], "ur",%f) xtitle("interpolação por spline (derivadas)") subplot(3,1,3) plot2d(xx, [yy2k yy2f]) legends(["spline não é um nó","sub-spline rápido"], [1 2], "lr",%f) xtitle("interpolação por splines (segundas derivadas)")
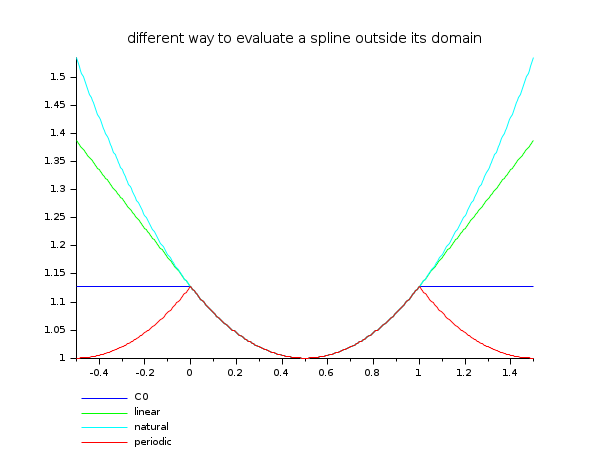
// aqui está um exemplo mostrando as diferentes possibilidades de extrapolação x = linspace(0,1,11)'; y = cosh(x-0.5); d = splin(x,y); xx = linspace(-0.5,1.5,401)'; yy0 = interp(xx,x,y,d,"C0"); yy1 = interp(xx,x,y,d,"linear"); yy2 = interp(xx,x,y,d,"natural"); yy3 = interp(xx,x,y,d,"periodic"); clf() plot2d(xx,[yy0 yy1 yy2 yy3],style=2:5,frameflag=2,leg="C0@linear@natural@periodic") xtitle(" Modos diferentes de avaliar um spline fora de seu domínio")
Ver Também
| Report an issue | ||
| << eval_cshep2d | Interpolação | interp1 >> |