Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
dsearch
指定の分類で行列またはハイパー行列の要素を分配, 配置および数える
呼び出し手順
[i_bin [,counts [,outside]]] = dsearch(X, bins ) [i_bin [,counts [,outside]]] = dsearch(X, bins , pm )
引数
- X
実数,エンコードされた整数,またはテキストの行列またはハイパー行列: 分類するエントリ. 複素数と多項式はサポートされません.
- bins
分類を定義する
Xと同じ型 (Xのエンコードされた整数の場合,binsは10進数とすることができます) の行または列ベクトル,- 離散型の場合(pm="d"):
binsは,Xのエントリを特定する異なった値となります. IfXが数値 (実数またはエンコードされた整数)の場合,binsは厳密に昇順にソートする必要があります. - 連続の場合 (デフォルト, pm="c"):
binsは 隣接する間隔の境界です:I1 = [bins(1), bins(2)],I2 = (bins(2), bins(3)],...,In = (bins(n), bins(n+1)].Xからのエントリはbins(1)に等しいものがI1に含まれることに注意してください.binsの値は厳密に昇順である必要があります: bins(1) < bins(2) < ... < bins(n). テキスト処理の場合, 大文字小文字を区別する辞書順が使用されます.
- 離散型の場合(pm="d"):
- pm
"c" (連続, デフォルト) または "d" (離散): 処理モード. 連続モードの場合,
binsは分類として隣接する範囲の境界を定義します. 離散モードの場合,binsはXを特定する エントリの値を提供します.- i_bin
Xと同じ大きさの行列またはハイパー行列:i_bin(k)はX(k)が属する分類の添字です.X(k)がどの分類にも属さない場合,i_bin(k) = 0となります.- counts
- 各ビンにおけるXエントリの数.
連続ケース (pm="c"): counts(i)は, 上記 (
binsパラメータ参照)の範囲Ikに属するXの要素数です. bins(1)にちょうど等しいXの要素はcounts(1)に含まれます.countsの大きさはbins- 1 です.離散ケース(pm="d"):
counts(i)は,bins(i)に等しいXの要素の数です. - outside
binsのどれにも属さないXのエントリの総数.
説明
各X(i)エントリについて,
dsearchは,binsにより定義される
値bins(j)または
範囲(bins(j), bins(j+1)] について
X(i)を含まれるまたは等しいかを決めます.
その後, 等しいビンがないまたは有する場合に応じて,
i_bin(i) = j または 0 を返します.
(最初の範囲がbins(1)を含みます)
各ビンの母集団がcountsにより返されます.
ビンに含まれないエントリの総数がoutside に返されます
(よってoutside = sum(bool2s(i_bin==0))です).
dsearch(..) はオーバーロードできます.
デフォルト pm="c" オプションはデータ集合を与える関数の実験的なヒストグラムを計算する
際に使用できます.
例
// DISCRETE values of TEXT // ----------------------- i = grand(4,6,"uin",0,7)+97; T = matrix(strsplit(ascii(i),1:length(i)-1), size(i)); T(T=="f") = "#"; T(T=="a") = "AA"; T bins = [ strsplit(ascii(97+(7:-1:0)),1:7)' "AA"] [i_bin, counts, outside] = dsearch(T, bins, "d") // BINNING TEXTS in LEXICOGRAPHIC INTERVALS // ---------------------------------------- // generating a random matrix of text nL = 3; nC = 5; L = 3; s = ascii(grand(1,nL*nC*L,"uin",0,25)+97); T = matrix(strsplit(s, L:L:nL*nC*L-1), nL, nC); // generating random bins bounds L = 2; nC = 6; s = ascii(grand(1,nC*L,"uin",0,25)+97); bins = unique(matrix(strsplit(s, L:L:nC*L-1), 1, nC)) T [i_bin, counts, outside] = dsearch(T, bins)
以下の例では, 3つの範囲
I1 = [5,11],
I2 = (11,15] および I3 = (15,20]を考えます.
X = [11 13 1 7 5 2 9]のエントリの位置をこれらの範囲で探してみます.
[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
表示される出力:
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
outside =
2.
counts =
4. 1. 0.
i_bin =
1. 2. 0. 1. 1. 0. 1.
ここで,
X(1)=11 は範囲 I1, すなわち i_bin(1)=1.
X(2)=13 は範囲 I2, すなわち i_bin(2)=2.
X(3)=1 は定義された範囲のどれにも属さない, すなわち i_bin(3)=0.
X(4)=7 は範囲 I1, すなわち i_bin(4)=1.
...
I1 には4個のエントリ (5, 7, 9 および 11), すなわち counts(1)=4.
I2 のエントリは1個のみ (13), すなわち counts(2)=1.
I3 にはXのエントリなし, すなわち counts(3)=0.
2個のXのエントリは定義された範囲のどれにも属さない(1, 2), すなわち outside=2.
// Numbers in DISCRETE categories (having specific values) // ------------------------------ [i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20],"d" )
は以下を出力します
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20], "d" )
outside =
5.
counts =
1. 1. 0. 0.
i_bin =
2. 0. 0. 0. 1. 0. 0.
ここで,
X(1)=11 は位置 #2にある集合
bins, すなわち i_bin(1)=2.X(2)=13 は集合
binsに含まれない, すなわち i_bin(2)=0....
X(7)=9 は集合
binsに含まれない, すなわち i_bin(7)=0.5に等しいXのエントリ(5)は1つのみ, すなわち, counts(1)=1.
bins(4)に一致するエントリはなし, すなわち counts(4)=0.集合
binsに含まれないXのエントリは5個(すなわち 13, 1, 7, 2, 9), よってoutside=5.
処理モード(連続または離散)によらず
binsの数は昇順にする必要があります.
これ以外の場合, エラーが発生します:
-->dsearch([11 13 1 7 5 2 9], [2 1])
!--error 999
dsearch : the array s (arg 2) is not well ordered
-->dsearch([11 13 1 7 5 2 9], [2 1],"d")
!--error 999
dsearch : the array s (arg 2) is not well ordered
高度な例
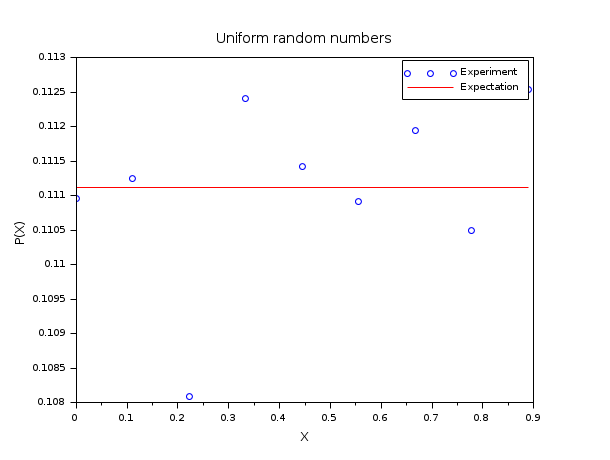
以下の例では, [0,1) の一様乱数の経験的ヒストグラムを一様分布関数と比較します. この比較を行うために, 範囲(pm="c")に基づくデフォルトの探索アルゴリズムを 使用します. Xを [0,1)の範囲の一様乱数の集合(m=50 000)として生成します. n=10とし,[0,1]の範囲に等間隔の値を配置し, 関連する範囲を設定します. 次に,各範囲に入るXのエントリの数を数えます: これは,一様分布関数の経験的ヒストグラムです. 数/mの期待値は 1/(n-1) に等しくなります.
m = 50000 ; n = 10; X = grand(m, 1, "def"); bins = linspace(0, 1, n)'; [i_bin, counts] = dsearch(X, bins); e = 1/(n-1)*ones(1, n-1); scf() ; plot(bins(1:n-1), counts/m, "bo"); plot(bins(1:n-1), e', "r-"); legend(["Experiment", "Expectation"]); xtitle("Uniform random numbers", "X", "P(X)");
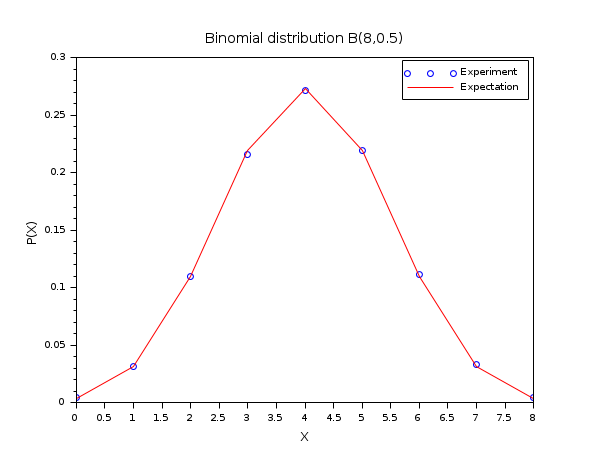
以下の例では,二項分布乱数のヒストグラムを N=8 および p=0.5の二項確率分布関数B(N,p)と比較します. この比較を行うために, 集合に基づく離散アルゴリズム(pm="d")を使用します.
N = 8 ; p = 0.5; m = 50000; X = grand(m,1,"bin",N,p); bins = (0:N)'; [i_bin, counts] = dsearch(X, bins, "d"); Pexp = counts/m; Pexa = binomial(p,N); scf() ; plot(bins, Pexp, "bo"); plot(bins, Pexa', "r-"); xtitle("Binomial distribution B(8,0.5)","X","P(X)"); legend(["Experiment","Expectation"]);
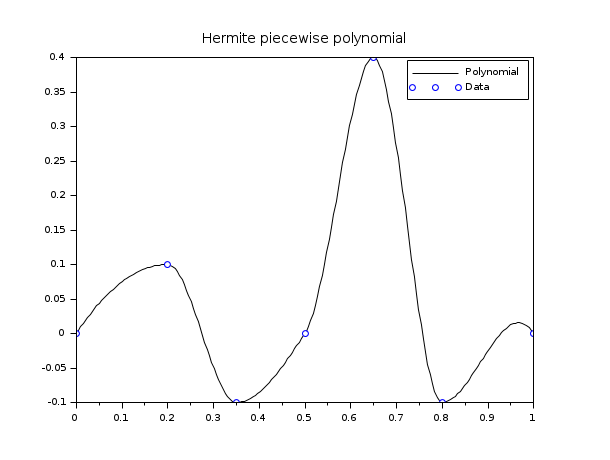
以下の例では,データ集合を補間するたねい離散エルミート多項式を使用します.
// define Hermite base functions function y=Ll(t, k, x) // Lagrange left on Ik y=(t-x(k+1))./(x(k)-x(k+1)) endfunction function y=Lr(t, k, x) // Lagrange right on Ik y=(t-x(k))./(x(k+1)-x(k)) endfunction function y=Hl(t, k, x) y=(1-2*(t-x(k))./(x(k)-x(k+1))).*Ll(t,k,x).^2 endfunction function y=Hr(t, k, x) y=(1-2*(t-x(k+1))./(x(k+1)-x(k))).*Lr(t,k,x).^2 endfunction function y=Kl(t, k, x) y=(t-x(k)).*Ll(t,k,x).^2 endfunction function y=Kr(t, k, x) y=(t-x(k+1)).*Lr(t,k,x).^2 endfunction x = [0 ; 0.2 ; 0.35 ; 0.5 ; 0.65 ; 0.8 ; 1]; y = [0 ; 0.1 ;-0.1 ; 0 ; 0.4 ;-0.1 ; 0]; d = [1 ; 0 ; 0 ; 1 ; 0 ; 0 ; -1]; X = linspace(0, 1, 200)'; i_bin = dsearch(X, x); // plot the curve Y = y(i_bin).*Hl(X,i_bin) + y(i_bin+1).*Hr(X,i_bin) + d(i_bin).*Kl(X,i_bin) + d(i_bin+1).*Kr(X,i_bin); scf(); plot(X,Y,"k-"); plot(x,y,"bo") xtitle("Hermite piecewise polynomial"); legend(["Polynomial","Data"]); // NOTE : it can be verified by adding these ones : // YY = interp(X,x,y,d); plot2d(X,YY,3,"000")
参照
履歴
| バージョン | 記述 |
| 5.5.0 | ハイパー行列, エンコードされた整数,およびテキストへの拡張. |
| Report an issue | ||
| << searchandsort | searchandsort | find >> |