Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
dsearch
répartit, localise et compte les éléments d'une matrice en catégories données
Séquence d'appel
[i_bin [,counts [,outside]]] = dsearch(X, bins ) [i_bin [,counts [,outside]]] = dsearch(X, bins , pm )
Paramètres
- X
matrice ou hypermatrice de nombres réels, d'entiers encodés, ou de textes : éléments à catégoriser. Les nombres complexes et les polynômes ne sont pas admis.
- bins
vecteur ligne ou colonne définissant les catégories, de même type que
X(SiXcontient des entiers encodés,binspeut être de type décimal).- Cas discret (pm="d"):
binscontient les valeurs auxquelles les éléments deXdoivent être identifiés. SiXest numérique (nombres réels ou entiers encodés),binsdoit être préalablement trié par ordre croissant, et sans doublons. - Cas continu (par défaut, pm="c"):
binscontient les bornes d'intervallesIkcontigus :I1 = [bins(1), bins(2)],I2 = (bins(2), bins(3)],...,In = (bins(n), bins(n+1)]. Noter queI1est fermé à gauche, alors que lesI(k>1)sont semi-ouverts à gauche. Les bornesbinsdoivent être préalablement triées en ordre strictement croissant : bins(1) < bins(2) < ... < bins(n). Pour le traitement du texte, l'ordre lexicographique sensible à la casse est considéré.
- Cas discret (pm="d"):
- pm
"c" (continu, par défaut) ou "d" (discrêt): mode de traitement. En mode continu,
binsspécifie les bornes d'intervalles contigus définissant les catégories à considérer. En mode discrêt,binsfournit les valeurs auxquelles les éléments deXdoivent être individuellement identifiés.- i_bin
Matrice ou hypermatrice de mêmes tailles que
X:i_bin(k)donne le n° de la catégorie à laquelleX(k)appartient. SiX(k)n'appartient à aucune catégorie,i_bin(k) = 0.- counts
- Nombre d'éléments de X dans les catégories respectives.
Cas continu(pm="c"): counts(i) éléments de
Xappartiennent à l'intervalleIktel que défini ci-dessus (voir le paramètrebins). Les éléments deXjuste égaux à bins(1) sont comptés dans counts(1).countsest un vecteur de même taille quebins, - 1.Cas discrêt(pm="d"):
counts(i)indique le nombre d'éléments deXégaux àbins(i) - outside
Nombre total d'éléments de X n'appartenant à aucune catégorie
bins.
Description
Pour chaque élément X(i), la fonction dsearch détermine la valeur bins(j) ou l'intervalle (bins(j), bins(j+1)] égale à ou contenant X(i). Elle retourne i_bin(i) = j, ou 0 si aucune valeur ou intervalle ne convient (le premier intervalle inclut bins(1) à gauche). L'effectif de chaque de chaque catégorie est retourné dans le vecteur counts. Le nombre d'éléments de X n'allant dans aucune catégorie est retourné dans outside (donc outside = sum(bool2s(i_bin==0))).
dsearch(..) peut être surchargée.
Le mode pm="c" par défaut peut être utilisé pour calculer l'histogramme empirique d'une fonction appliquée à un ensemble de points donnés.
Exemples
// TEXTES en valeurs PARTICULIERES // ------------------------------- i = grand(4,6,"uin",0,7)+97; T = matrix(strsplit(ascii(i),1:length(i)-1), size(i)); T(T=="f") = "#"; T(T=="a") = "AA"; T bins = [ strsplit(ascii(97+(7:-1:0)),1:7)' "AA"] [i_bin, counts, outside] = dsearch(T, bins, "d") // TEXTES categorisés par INTERVALLES LEXICOGRAPHIQUES // --------------------------------------------------- // Génération d'une matrice texte aléatoire nL = 3; nC = 5; L = 3; s = ascii(grand(1,nL*nC*L,"uin",0,25)+97); T = matrix(strsplit(s, L:L:nL*nC*L-1), nL, nC); // Génération d'intervalles lexicographiques aléatoires ordonnés L = 2; nC = 6; s = ascii(grand(1,nC*L,"uin",0,25)+97); bins = unique(matrix(strsplit(s, L:L:nC*L-1), 1, nC)) T [i_bin, counts, outside] = dsearch(T, bins)
Dans l'exemple suivant, considérons 3 intervalles I1 = [5,11],
I2 = (11,15] and I3 = (15,20].
Nous recherchons les n° des intervalles respectifs auxquels les éléments de X = [11 13 1 7 5 2 9] appartiennent.
[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
Résultat affiché :
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20])
outside =
2.
counts =
4. 1. 0.
i_bin =
1. 2. 0. 1. 1. 0. 1.
En effet,
X(1)=11 est dans l'intervalle I1, donc i_bin(1)=1.
X(2)=13 est dans l'intervalle I2, donc i_bin(2)=2.
X(3)=1 n'appartient à aucun des intervalles définis, donc i_bin(3)=0.
X(4)=7 est dans l'intervalle I1, donc i_bin(4)=1.
...
4 éléments de X (5, 7, 9 et 11) appartiennent à I1, donc counts(1)=4.
Seul un élément de X (13) est dans I2, donc counts(2)=1.
Aucun élément de X est dans I3, donc counts(3)=0.
Deux éléments de X (i.e. 1, 2) n'appartiennent à aucun intervalle défini, donc outside=2.
// Nombres à identifier à des valeurs discrêtes // -------------------------------------------- [i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20],"d" )
affiche
-->[i_bin, counts, outside] = dsearch([11 13 1 7 5 2 9], [5 11 15 20], "d" )
outside =
5.
counts =
1. 1. 0. 0.
i_bin =
2. 0. 0. 0. 1. 0. 0.
En effet,
X(1)=11égalebins(2), donci_bin(1)=2.X(2)=13ne correspond à aucune des valeurs debins, donci_bin(2)=0....
X(7)=9ne correspond à aucune des valeurs debins, donci_bin(7)=0.Un seul élément de X vaut
bin(1)=5, donccounts(1)=1.Aucun élément de X ne vaut
bins(4)=20, donccounts(4)=0.5 éléments de X (i.e. 13, 1, 7, 2, 9) ne sont identiables à aucun des éléments de
bins, doncoutside=5.
Les nombres dans bins doivent être rangés par ordre strictement croissant, que le mode de traitement soit continu ou discrêt. Dans le cas contraire, une erreur se produit.
-->dsearch([11 13 1 7 5 2 9], [2 1])
!--error 999
dsearch : the array s (arg 2) is not well ordered
-->dsearch([11 13 1 7 5 2 9], [2 1],"d")
!--error 999
dsearch : the array s (arg 2) is not well ordered
Exemples avancés
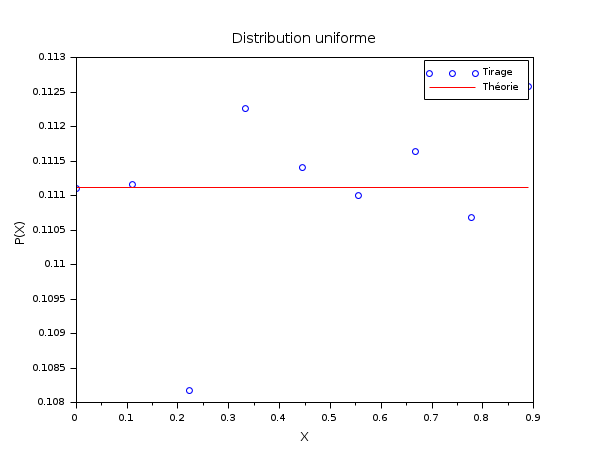
Dans l'exemple suivant, l'histogramme empirique d'un tirage aléatoire à distribution uniforme sur [0, 1] est comparé avec la fonction de distribution théorique uniforme. A cette fin, une catégorisation par intervalles contigus est utilisée (pm="c"). Une matrice X de m=50000 nombres aléatoires à ditribution uniforme sur [0,1[ sont générés. n=10 bornes régulièrement espacées sur [0,1] sont générées et partionnent ce domaine en n-1=9 intervalles de largeurs identiques. dsearch() classe et dénombre les effectifs de X dans chaque intervalle. La valeur de counts(i)/m attendue (pour m -> inf) vaut 1/(n-1).
m = 50000 ; n = 10; X = grand(m,1,"def"); bins = linspace(0,1,n)'; [i_bin, counts] = dsearch(X, bins); e = 1/(n-1)*ones(1,n-1); scf() ; plot(bins(1:n-1), counts/m,"bo"); plot(bins(1:n-1), e',"r-"); legend(["Experiment","Expectation"]); xtitle("Uniform random numbers","X","P(X)");
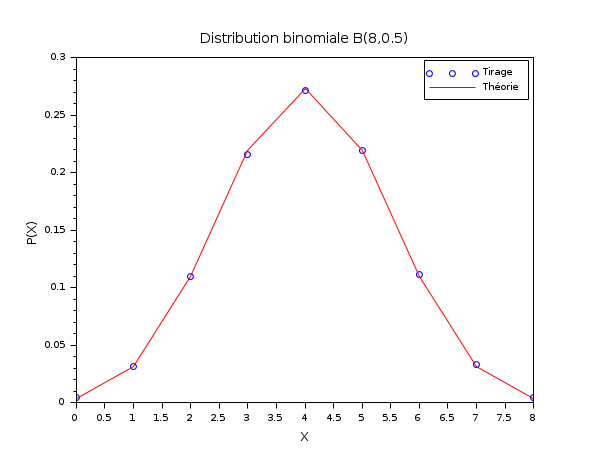
Dans l'exemple suivant, l'histogramme d'un tirage aléatoire à distribution binomiale est comparé avec la fonction de distribution de probabilité binomiale théorique B(N,p), avec N=8 et p=0.5. A cette fin, dsearch() est utilisée en mode discret ("pm="d").
N = 8 ; p = 0.5; m = 50000; X = grand(m,1,"bin",N,p); bins = (0:N)'; [i_bin, counts] = dsearch(X, bins, "d"); Pexp = counts/m; Pexa = binomial(p,N); scf() ; plot(bins, Pexp, "bo"); plot(bins, Pexa', "r-"); xtitle("Distribution binomiale B(8,0.5)","X","P(X)"); legend(["Tirage","Théorie"]);
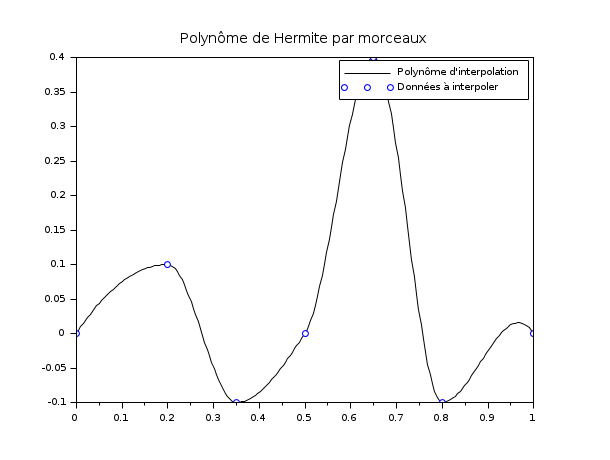
Autre exemple : utilisons maintenant une série de polynômes de Hermite définis par morceaux pour interpoler un ensemble depoints.
// Définition de la base des fonctions de Hermite : function y=Ll(t, k, x) // Lagrange left on Ik y=(t-x(k+1))./(x(k)-x(k+1)) endfunction function y=Lr(t, k, x) // Lagrange right on Ik y=(t-x(k))./(x(k+1)-x(k)) endfunction function y=Hl(t, k, x) y=(1-2*(t-x(k))./(x(k)-x(k+1))).*Ll(t,k,x).^2 endfunction function y=Hr(t, k, x) y=(1-2*(t-x(k+1))./(x(k+1)-x(k))).*Lr(t,k,x).^2 endfunction function y=Kl(t, k, x) y=(t-x(k)).*Ll(t,k,x).^2 endfunction function y=Kr(t, k, x) y=(t-x(k+1)).*Lr(t,k,x).^2 endfunction x = [0 ; 0.2 ; 0.35 ; 0.5 ; 0.65 ; 0.8 ; 1]; y = [0 ; 0.1 ;-0.1 ; 0 ; 0.4 ;-0.1 ; 0]; d = [1 ; 0 ; 0 ; 1 ; 0 ; 0 ; -1]; X = linspace(0, 1, 200)'; i_bin = dsearch(X, x); // Affichage de la courbe : Y = y(i_bin).*Hl(X,i_bin) + y(i_bin+1).*Hr(X,i_bin) + d(i_bin).*Kl(X,i_bin) + d(i_bin+1).*Kr(X,i_bin); scf(); plot(X,Y,"k-"); plot(x,y,"bo") xtitle("Polynôme de Hermite par morceaux"); legend(["Polynôme d''interpolation","Données à interpoler"]); // NOTE : pour vérifier, décommenter et exécuter la ligne suivante // YY = interp(X,x,y,d); plot2d(X,YY,3,"000")
Voir aussi
Historique
| Version | Description |
| 5.5.0 | Extension aux hypermatrices, aux entiers encodés, et au traitement du texte. |
| Report an issue | ||
| << Chercher et trier | Chercher et trier | find >> |