- Aide de Scilab
- Graphiques
- 2d_plot
- champ
- champ1
- champ properties
- comet
- contour2d
- contour2di
- contour2dm
- contourf
- cutaxes
- errbar
- fchamp
- fec
- fec properties
- fgrayplot
- fplot2d
- grayplot
- grayplot properties
- graypolarplot
- histplot
- LineSpec
- loglog
- Matplot
- Matplot1
- Matplot properties
- paramfplot2d
- plot
- plot2d
- plot2d2
- plot2d3
- plot2d4
- plotimplicit
- polarplot
- scatter
- semilogx
- semilogy
- Sfgrayplot
- Sgrayplot
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
histplot
dessine un histogramme
Syntaxe
histplot(n, data [,normalization] [,polygon], <opt_args>) histplot(x, data [,normalization] [,polygon], <opt_args>) cf = histplot(..)
Arguments
- n
entier strictement positif (nombre de classes)
- x
vecteur (strictement croissant) definissant les classes
- data
vecteur (contenant les données à analyser)
- <opt_args>
Représente une séquence de la forme
clé1=valeur1, clé2=valeur2,... oùclé1,clé2,...peut être n'importe quel paramètre optionnel de plot2d (style,strf,leg, rect,nax, logflag,frameflag, axesflag) ou encorenormalization. Pour ce dernier la valeur correspondante est un scalaire booléen (la valeur par défaut étant %t).- cf
Fréquences calculées (hauteurs de l'histogramme)
Description
Cette fonction dessine un histogramme des données contenues dans le vecteur data
en utilisant les classes x. Quand le nombre de classes n est fourni
au lieu de x, celles-ci sont définies de manière équirépartie et telles que
x(1) = min(data) < x(2) = x(1) + dx < ... < x(n+1) = max(data)
avec dx = (x(n+1)-x(1))/n.
Les classes sont définies par C1 = [x(1), x(2)] puis Ci = ] x(i), x(i+1)] pour i = 2,3,...,n.
En notant Nmax le nombre total de données (Nmax = length(data)) et Ni le nombre de données
se situant dans Ci, la valeur de l'histogramme pour x appartenant à Ci
est égale à Ni/(Nmax (x(i+1)-x(i))) quand normalization est vrai
(comportement par défaut) et sinon elle vaut simplement Ni. Quand l'histogramme
est normalisé il vérifie la propriété suivante :
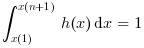
quand x(1)<=min(data) et max(data) <= x(n+1)
N'importe quel paramètre optionnel de plot2d peut être passé à histplot ; par exemple
pour dessiner votre histogramme avec la couleur numéro 2 (du bleu si vous utilisez la carte
des couleurs standard) tout en restreignant le dessin au le rectangle [-3,3]x[0,0.5],
vous pouvez utiliser histplot(n,data, style=2, rect=[-3,0,3,0.5]).
La commande histplot() sans argument montre un example.
Exemples
Exemple n°1 : variations sur l'histogramme d'un échantillon gaussien N(0,1)
d = rand(1,10000,'normal'); clf(); histplot(20,d); clf(); histplot(20,d,normalization=%f); clf(); histplot(20,d,leg='rand(1,10000,''normal'')',style=5); clf(); histplot(20,d,leg='rand(1,10000,''normal'')',style=16, rect=[-3,0,3,0.5]);
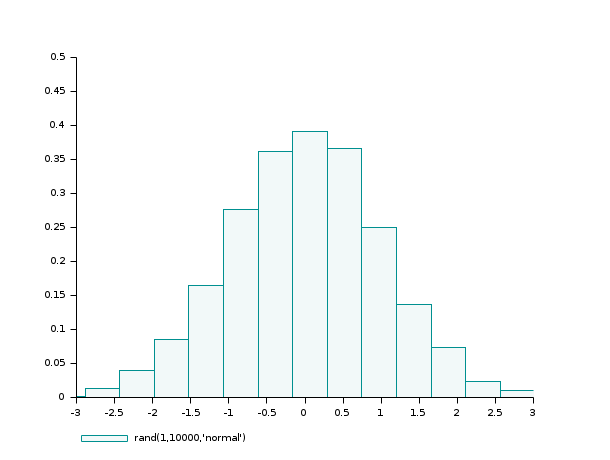
Exemple n°2 : histogramme d'un échantillon de loi binomiale B(6,0.5)
d = grand(1000,1,"bin", 6, 0.5); c = linspace(-0.5,6.5,8); clf() subplot(2,1,1) histplot(c, d, style=2); xtitle("l''histogramme normalisé") subplot(2,1,2) histplot(c, d, normalization=%f, style=5); xtitle("l''histogramme non normalisé")
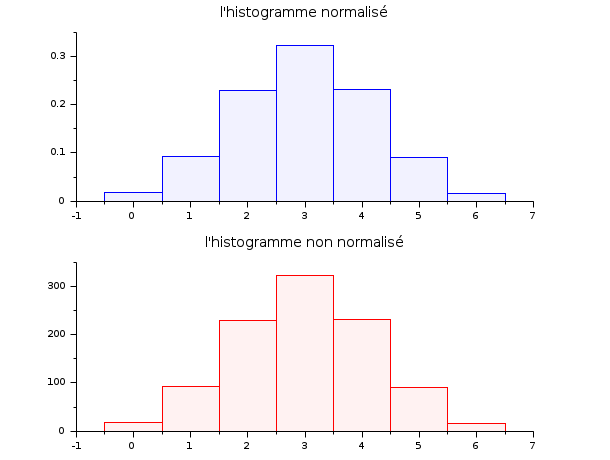
Exemple n°3 : histogramme d'un échantillon de loi exponentielle E(lambda)
lambda = 2; X = grand(100000,1,"exp", 1/lambda); Xmax = max(X); clf() histplot(40, X, style=2); x = linspace(0,max(Xmax),100)'; plot2d(x,lambda*exp(-lambda*x),strf="000",style=5) legend(["histogramme d''un échantillon E(lambda)" "densité exacte"]);
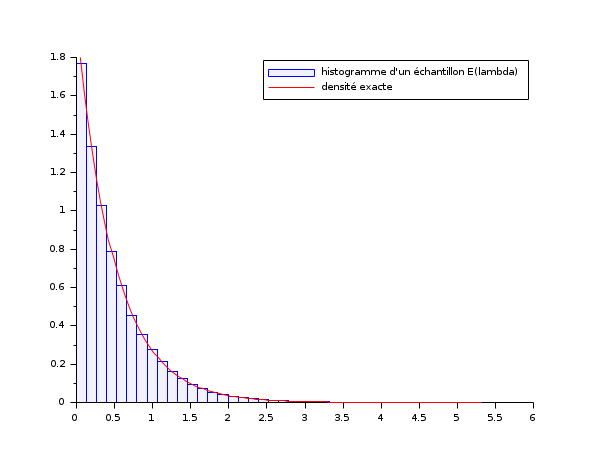
Exemple n°4 : courbe des fréquences empiriques et histogramme d'un échantillon aléatoire gaussien.
n = 10; data = rand(1,1000,"normal"); clf(); histplot(n, data, style=12, polygon=%t); legend(["Histogramme normalisé" "Courbe des fréquences"],"lower_caption");

Voir aussi
Historique
| Version | Description |
| 5.5.0 | Ajout de l'option polygon et de la sortie cf. |
| Report an issue | ||
| << graypolarplot | 2d_plot | LineSpec >> |