odedc

Arguments

y0

a real column vector (initial conditions), y0=[y0c;y0d] where y0d has nd components.

nd

an integer, dimension of y0d

stdel

a real vector with one or two entries, stdel=[h, delta] (with delta=0 as default value).

t0

a real scalar (initial time).

t

a real (row) vector, instants where yt is calculated.

f

an external i.e. a function or a character string or a list with syntax: yp = f(t,yc,yd,flag).

f

an external i.e. a function or a character string or a list with syntax: yp = f(t,yc,yd,flag)

a list

This form of external is used to pass parameters to the function. It must be as follows:

list(f, p1, p2,...)

where the syntax of the function f is now

yp = f(t, yc, yd, flag, p1, p2,...)

f still returns the function value as a function of (t, yc, yd, flag, p1, p2,...), and p1, p2,... are function parameters.

a character string

it must refer to the name of a C or fortran routine, assuming that <f_name> is the given name.

• The Fortran calling sequence must be

  <f_name>(iflag, nc, nd, t, y, ydp)

  double precision t, y(*), ydp(*)

  integer iflag, nc, nd

• The C syntax must be

  void <f_name> (int *iflag, int *nc, int *nd, double *t, double *y, double *ydp)

In both Fortran and C cases, the input arguments are:

• iflag = 0 or 1

• nc = number of continuous states yc

• nd = number of discrete states yd

• t = time

• y = [yc; yd; param]. param may be used to get extra arguments which have been given in the odedc call (y = odedc([y0c; y0d], nd, stdel, t0, t, list('fexcd', param)))

• As output ydp, the routine must compute ydp[0:nc-1] = d/dt ( yc(t) ) for iflag=0 and ydp[0:nd-1] = yd(t+) for iflag=1.

Description

y = odedc([y0c;y0d], nd, [h,delta], t0, t, f) computes the solution of a mixed discrete/continuous system. The discrete system state ydk is embedded into a piecewise constant yd(t) time function as follows: yd(t) = ydk for t in [tk = h*(delta+k) , tk+1 = h*(delta+k+1) ).

The simulated equations are now, for t in [ t_k , t_k+1 ):

dyc/dt = f(t, yc(t), yd(t), 0)
yc(t0) = y0c

and at instants tk the discrete variable yd is updated by

yd(tk+) = f(yc(tk-), yd(tk-), 1).

Note that, using the definition of yd(t) the last equation gives

ydk = f(tk, yc(tk-), yd(tk-1), 1)

(yc is time-continuous: yc(tk-) = yc(tk)).

The calling parameters of f are fixed: ycd = f(t,yc,yd,flag); this function must return either the derivative of the vector yc if flag=0 or the update of yd if flag=1.

ycd = dot(yc) must be a vector with same dimension as yc if flag=0 and ycd = update(yd) must be a vector with same dimension as yd if flag=1.

t is a vector of instants where the solution y is computed.

y is the vector y = [y(t(1)), y(t(2)),...].

This function can be called with the same optional parameters as the ode function (provided nd and stdel are given in the syntax as second and third parameters). In particular integration flags, tolerances can be set. Optional parameters can be set by the odeoptions function.

External routines can be dynamically linked (see link).

Examples

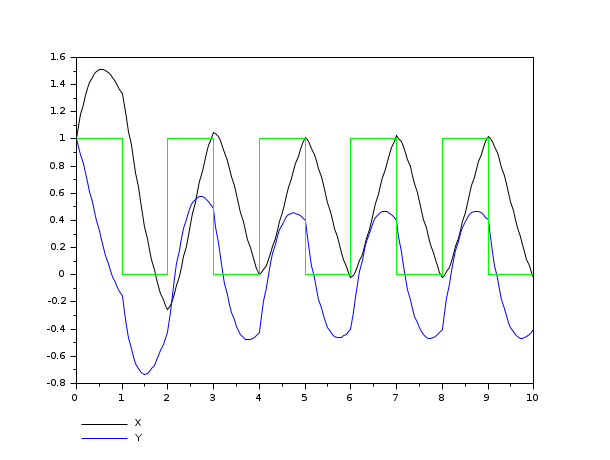
//Linear system with switching input
deff('xdu = phis(t,x,u,flag)', 'if flag==0 then xdu=A*x+B*u; else xdu=1-u; end');
x0 = [1;1];
A = [-1,2;-2,-1];
B = [1;2];
u = 0;
nu = 1;
stdel = [1,0];
u0 = 0;
t = 0:0.05:10;
xu = odedc([x0;u0], nu, stdel, 0, t, phis);
x = xu(1:2,:);
u = xu(3,:);
nx = 2;
plot2d(t, x', [1:nx], '161')
plot2d2('onn', t', u', [nx+1:nx+nu], '000');
//Fortran external (see fydot2.f):
norm(xu - odedc([x0;u0], nu, stdel, 0, t, 'phis'), 1)

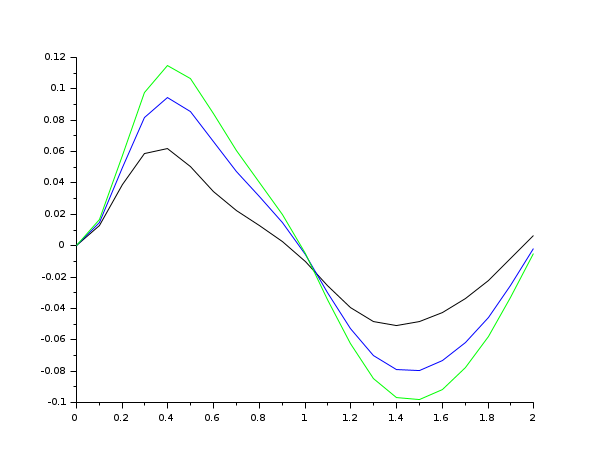
//Sampled feedback
//
//        |     xcdot=fc(t,xc,u)
//  (system)   |
//        |     y=hc(t,xc)
//
//
//        |     xd+=fd(xd,y)
//  (feedback) |
//        |     u=hd(t,xd)
//
deff('xcd = f(t,xc,xd,iflag)',...
  ['if iflag==0 then '
   '  xcd=fc(t,xc,e(t)-hd(t,xd));'
   'else '
   '  xcd=fd(xd,hc(t,xc));'
   'end']);
A = [-10,2,3;4,-10,6;7,8,-10];
B = [1;1;1];
C = [1,1,1];
Ad = [1/2,1;0,1/20];
Bd = [1;1];
Cd = [1,1];
deff('st = e(t)', 'st = sin(3*t)')
deff('xdot = fc(t,x,u)', 'xdot = A*x+B*u')
deff('y = hc(t,x)', 'y = C*x')
deff('xp = fd(x,y)', 'xp = Ad*x + Bd*y')
deff('u = hd(t,x)', 'u = Cd*x')
h = 0.1; t0=0; t=0:0.1:2;
x0c = [0;0;0];
x0d = [0;0];
nd = 2;
xcd = odedc([x0c;x0d], nd, h, t0, t, f);
norm(xcd - odedc([x0c;x0d], nd, h, t0, t, 'fcd1')) // Fast calculation (see fydot2.f)
plot2d([t',t',t'], xcd(1:3,:)');
scf(2);
plot2d2("gnn", [t',t'], xcd(4:5,:)');
scf(0);

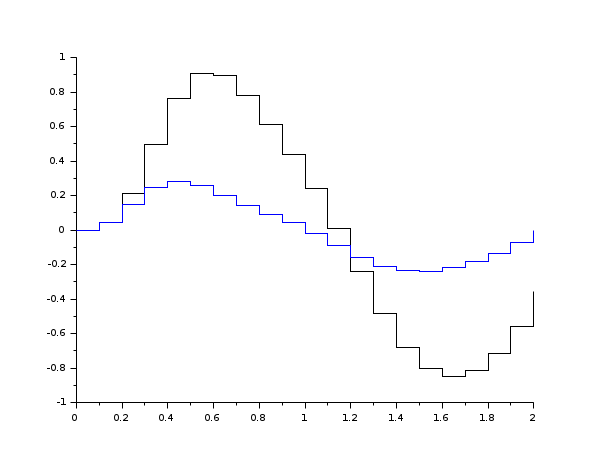
See also

• ode — ordinary differential equation solver
• link — dynamic linker
• odeoptions — set options for ode solvers
• csim — simulation (time response) of linear system
• external — Scilab Object, external function or routine