Scilab-Branch-6.1-GIT
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
integrate
integration of an expression by quadrature
Syntax
y = integrate(expr, v, x0, x1) y = integrate(expr, v, x0, x1, atol) y = integrate(expr, v, x0, x1, atol, rtol)
Arguments
- expr
- a character string defining a Scilab expression.
- v
- a character string, the integration variable name.
- x0
- a real number, the lower bound of integration.
- x1
- a vector of real numbers, upper bounds of integration.
- atol
- a real number (absolute error bound). Default value: 1e-13.
- rtol
- a real number, (relative error bound). Default value: 1e-8.
- y
- a vector of real numbers, the integral value for each
x1(i).
Description
y = integrate(expr, v, x0, x1 [,atol [,rtol]]) computes
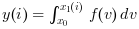 for
for i=1:size(x1,'*'), where f(v)
is given by the expression expr.
The evaluation hopefully satisfies following claim for accuracy:
abs(I - y) <= max(atol, rtol*abs(I)) where
I stands for the exact value of the integral.
 | Restriction: The given expression must not use variable names with a leading
%. |
Examples
See also
History
| Version | Description |
| 6.1.0 | Default atol value increased from 10-14 to 10-13. |
| Report an issue | ||
| << intc | Differential calculus, Integration | intg >> |