Scilab-Branch-6.1-GIT
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
integrate
intégration numérique d'une expression
Séquence d'appel
y = integrate(expr, v, x0, x1) y = integrate(expr, v, x0, x1, atol) y = integrate(expr, v, x0, x1, atol, rtol)
Paramètres
- expr
- chaîne de caractères : expression scilab fournissant l'intégrande.
- v
- chaîne de caractères : nom de la variable d'intégration.
- x0
- nombre réel, la borne inférieure de l'intégration.
- x1
- vecteur de nombres réels, les bornes supérieures d'intégration.
- atol
- nombre réel positif: erreur absolue maximale acceptable. Par défaut : 1d-13
- rtol
- nombre réel positif: erreur relative maximale acceptable. Par défaut : 1d-8
- y
- vecteur de nombres réels, la valeur de l'intégrale pour chaque
x1(i).
Description
calcule
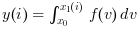 pour
pour i=1:size(x1,'*'),
où f(v) est donnée par l'expression expr.
L'approximation satisfait (on l'espère) l'affirmation suivante sur l'erreur :
abs(I-y) <= max(atol, rtol*abs(I))
où I représente la valeur exacte de l'intégrale.
 | Restriction : l'expression fournie ne doit pas contenir de noms de variables
commençant par %. |
Exemples
Voir aussi
Historique
| Version | Description |
| 6.1.0 | Valeur par défaut de atol : 10-13 (au lieu de 10-14). |
| Report an issue | ||
| << intc | Intégration - dérivation | intg >> |