Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
numderivative
approximation des dérivées d'une fonction (matrices jacobienne ou hessienne)
Séquence d'appel
J = numderivative(f, x) J = numderivative(f, x, h) J = numderivative(f, x, h, order) J = numderivative(f, x, h, order, H_form) J = numderivative(f, x, h, order, H_form, Q) [J, H] = numderivative(...)
Paramètres
- f
une fonction ou une liste, la fonction à différencier.
- x
un vecteur de réels n-par-1 ou 1-par-n, le point où calculer la dérivée.
- h
un vecteur de réels 1-par-1 ou n-par-1, le pas utilisé dans les approximations aux différences finies. Si
hn'est pas fourni, alors le pas par défaut est calculé suivantxet l'ordre,order. Sihest une matrice 1-par-1, elle est étendue à la même taille quex.- order
une matrice d'entiers positifs 1-par-1, l'ordre de la formule de différences finies (par défaut,
order=2). Les valeurs possibles deordersont 1, 2 et 4.- H_form
une chaîne de caractères, la forme sous laquelle la matrice hessienne est souhaitée en retour (par défaut,
H_form="default").Les valeurs possibles sont "default", "blockmat" et "hypermat". Voir la section "Forme de la matrice hessienne" ci-dessous pour des détails sur cette option.
- Q
une matrice de réels, modifie la direction de différenciation (par défaut,
Q=eye(n,n)). La matriceQdoit être orthogonale. Q fournit la possibilité de retirer l'arbitrarité de l'utilisation de la base canonique pour approximer les dérivées de la fonction.- J
une matrice réelle m-par-n, l'approximation de la matrice jacobienne. La ligne
J(k, :)approche le gradient defk, pourk = 1, 2, ..., m.- H
une matrice réelle, l'approximation de la matrice hessienne. Les éléments de
Happrochent les dérivées partielles de second ordre def.
Description
Calcule une approximation des matrices jacobienne et hessienne d'une fonction par différences finies.
La fonction f prend comme paramètre d'entrée
x, un vecteur n-par-1,
et retourne y, un vecteur m-par-1.
Dans la suite, la k-ème composante de f
est notée fk et la matrice hessienne de
fk est notée Hk,
pour k = 1, 2, ..., m.
Tout paramètre égal à la matrice vide []
sera remplacé par sa valeur par défaut.
En général, la formule découlant de order=1
fournit une erreur maximale (la moins précise), la formule de order = 2 fournit une erreur
moyenne et la formule order=4 la plus faible erreur (la plus précise).
Cela est faux dans certains cas : voir la section "Problèmes de précision" ci-dessous
pour plus de détails.
Les dérivées secondes sont calculées par composition des dérivées du premier ordre.
La fonction
La fonction f doit avoir le prototype suivant :
y = f (x)
où
- x
un vecteur de réels n-par-1, le point actuel
- y
un vecteur de réels m-par-1, la valeur de la fonction
Il se peut que la fonction requière des paramètres additionnels pour être évaluée.
Dans ce cas, on peut utiliser la fonctionnalité suivante.
Le paramètre f peut aussi être une liste (myfun, a1, a2, ...).
Dans ce cas, myfun, le premier élément de la liste, doit être une fonction au prototype :
y = myfun (x, a1, a2, ...)
a1, a2, ...
sont concaténés automatiquement à la fin de la séquence d'appel.Forme de la matrice hessienne
L'option H_form change les dimensions du paramètre de sortie
H.
Elle gère le cas général où m est différent de 1,
c'est-à-dire quand il y a plusieurs fonctions à différencier en même temps.
Les valeurs possibles de H_form sont :
- H_form = "default" :
H est une matrice
m-par-(n^2); sous cette forme, la ligneH(k, :)contientHk:H(k, :) == Hk(:)'- H_form = "blockmat" :
H est une matrice
(mn)-par-n: les matrices hessiennesn-par-nde chaque composante defsont stockées ligne par ligne, c'est-à-dire :H == [H1 ; H2 ; ... ; Hm]- H_form = "hypermat" :
H est une matrice n-par-n pour
m=1, et une hypermatrice n-par-n-par-m sinon. La matriceH(:, :, k)est la matrice hessienne de la k-ème composante def, i.e.H(:, :, k) == Hk
Performances
Si le problème est correctement dimensionné, augmenter l'ordre de la formule de différences finies peut réduire
l'erreur d'approximation mais requiert plus d'évaluations de la fonction.
La liste suivante présente le nombre d'évaluations nécéssaires au calcul du
Jacobien suivant l'ordre de la formule et la dimension de x,
notée n :
order = 1,n+1evaluations,order = 2,2névaluations,order = 4,4névaluations.
Calculer la matrice hessienne requiert le carré du nombre d'évaluations, comme détaillé ci-après :
order = 1,(n+1)^2évaluations (au total(n+1)^2+n+1),order = 2,4n^2évaluations (au total4n^2+2n),order = 4,16n^2évaluations (au total16n^2+4n).
Exemples
// La fonction à différencier function y=f(x) f1 = sin(x(1)*x(2)) + exp(x(2)*x(3)+x(1)) f2 = sum(x.^3) y = [f1; f2] endfunction // Le gradient exact function [g1, g2]=exactg(x) g1(1) = cos(x(1)*x(2))*x(2) + exp(x(2)*x(3)+x(1)) g1(2) = cos(x(1)*x(2))*x(1) + exp(x(2)*x(3)+x(1))*x(3) g1(3) = exp(x(2)*x(3) + x(1))*x(2) g2(1) = 3*x(1)^2 g2(2) = 3*x(2)^2 g2(3) = 3*x(3)^2 endfunction // La hessienne exacte function [H1, H2]=exactH(x) H1(1, 1) = -sin(x(1)*x(2))*x(2)^2 + exp(x(2)*x(3)+x(1)) H1(1, 2) = cos(x(1)*x(2)) - sin(x(1)*x(2))*x(2)*x(1) + exp(x(2)*x(3)+x(1))*x(3) H1(1, 3) = exp(x(2)*x(3)+x(1))*x(2) H1(2, 1) = H1(1, 2) H1(2, 2) = -sin(x(1)*x(2))*x(1)^2 + exp(x(2)*x(3)+x(1))*x(3)^2 H1(2, 3) = exp(x(2)*x(3)+x(1)) + exp(x(2)*x(3)+x(1))*x(3)*x(2) H1(3, 1) = H1(1, 3) H1(3, 2) = H1(2, 3) H1(3, 3) = exp(x(2)*x(3)+x(1))*x(2)^2 // H2(1, 1) = 6*x(1) H2(1, 2) = 0 H2(1, 3) = 0 H2(2, 1) = H2(1, 2) H2(2, 2) = 6*x(2) H2(2, 3) = 0 H2(3, 1) = H2(1, 3) H2(3, 2) = H2(2, 3) H2(3, 3) = 6*x(3) endfunction // Calcul du jacobien et de la hessienne x = [1; 2; 3]; J = numderivative(f, x) [J, H] = numderivative(f, x) // Comparaison avec les valeurs exactes [g1, g2] = exactg(x); Jexact = [g1'; g2'] [H1, H2] = exactH(x); Hexact = [H1(:)'; H2(:)'] // Configuration du pas J = numderivative(f, x, 1.e-1) // Configuration de l'ordre J = numderivative(f, x, [], 4) // Configuration de la forme de la hessienne [J, H] = numderivative(f, x, [], [], "blockmat") [J, H] = numderivative(f, x, [], [], "hypermat") // Configuration de Q n = 3; Q = qr(rand(n, n)) J = numderivative(f, x, [], [], [], Q) // Test des formules d'ordre 1, 2 et 4. // Pour la formule d'ordre 4, certaines entrées de H // sont calculées comme non-nulles. [g1, g2] = exactg(x); [H1, H2] = exactH(x); Jexact = [g1'; g2']; Hexact = [H1(:)'; H2(:)']; for i = [1, 2, 4] [J, H] = numderivative(f, x, [], i); dJ = floor(min(assert_computedigits(J, Jexact))); dH = floor(min(assert_computedigits(H, Hexact))); mprintf("ordre = %d, dJ = %d, dH = %d \n", i, dJ, dH); end
Paramètres additionnels
Dans l'exemple suivant, on utilise une fonction qui requiert le paramètre additionnel
p.
Soit, on utilise le fait que f puisse être une liste,
où le premier paramètre de la fonction
G et les éléments restants sont automatiquement passés
à la fonction.
La formule de Taylor
Si H est donnée sous sa forme par défaut, alors les séries de Taylor de
f(x) jusqu'aux termes de second ordre sont donnés par :
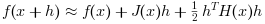
Dans le script suivant, on vérifié que cette formule à l'aide de différences finies.
// La fonction à différencier function y=f(x) f1 = sin(x(1)*x(2)) + exp(x(2)*x(3)+x(1)) f2 = sum(x.^3) y = [f1; f2] endfunction x = [1; 2; 3]; dx = 1e-3*[1; 1; -1]; [J, H] = numderivative(f, x); f(x+dx) f(x+dx)-f(x) f(x+dx)-f(x)-J*dx f(x+dx)-f(x)-J*dx-1/2*H*(dx .*. dx)
Dans l'exemple suivant, on utilise une fonction qui requiert trois paramètres additionnnels
A, p et w
// Un exemple trivial function y=f(x, A, p, w) y = x'*A*x + p'*x + w; endfunction // avec les matrices jacobienne et hessienne données par // J(x) = x'*(A+A')+p' et H(x) = A+A'. A = rand(3, 3); p = rand(3, 1); w = 1; x = rand(3, 1); h = 1; [J, H] = numderivative(list(f, A, p, w), x, h, [], "blockmat")
Problèmes de précision
Quand le pas h n'est pas fourni, la fonction numderivative
tente de calculer un pas qui donne une précision suffisante.
Ce pas dépend du degré des dérivées (jacobienne ou hessienne),
l'ordre de la formule et le point x.
Plus précisément, si x est non-nul,
alors le pas par défaut h est un vecteur de même taille que
x, dimensionné à la valeur absolue de
x.
Dans l'exemple suivant, on calcule la dérivée de la fonction racine carrée. Le script suivant affiche un graphe représentant l'erreur relative de la dérivée numérique en fonction du pas. On peut voir qu'il y a un pas optimal qui minimise l'erreur relative.
// Sa dérivée exacte function y=mydsqrt(x) y = 0.5 * x^(-0.5) endfunction x = 1.0; n = 1000; logharray = linspace (-16, 0, n); for i = 1:n h = 10^(logharray(i)); expected = mydsqrt(x); computed = numderivative (sqrt, x, h); relerr = abs(computed - expected) / abs(expected); logearray (i) = log10 (relerr); end scf(); plot (logharray, logearray); xtitle("Erreur relative de numderivative (x = 1.0)", .. "log(h)", "log(ER)");
La stratégie de numderivative fournit une précision suffisante dans
beaucoup de cas, mais peut ne pas être assez précise dans certains cas.
En fait, le pas optimal dépend aussi de la valeur de la fonction f(x)
et de sa dérivée seconde, lesquelles sont inconnues au moment ou le pas par défaut est calculé.
Voir "Practical optimization", par Gill, Murray et Wright, Academic Press, 1981,
pour plus de détails.
Les sections pertinentes sont "4.6.1. Finite-difference Approximations to First
Derivatives" et "8.6 Computing finite differences".
Historique
| Version | Description |
| 5.5.0 | Fonction numderivative introduite. |
| Report an issue | ||
| << inttrap | Intégration - dérivation | ode >> |