grand

Аргументы

m, n, o: целые числа, определяющие размеры матрицы/гиперматрицы Y.
X: матрица, у которой используются только её размеры (скажем m на n).
Y: матрица или гиперматрица со случайными элементами, зависящая от входных аргументов.
S: выходное значение действия (строка или вещественный вектор-столбец).

Описание

Эта функция формирует случайные числа по различным законам распределения.

Последовательности вызова:

Y = grand(m, n, "bet", A, B)
Y = grand(m, n, "bin", N, p)
Y = grand(m, n, "nbn", N, p)
Y = grand(m, n, "chi", Df)
Y = grand(m, n, "nch", Df, Xnon)
Y = grand(m, n, "exp", Av)
Y = grand(m, n, "f", Dfn, Dfd)
Y = grand(m, n, "nf", Dfn, Dfd, Xnon)
Y = grand(m, n, "gam", shape, rate)
Y = grand(m, n, "nor", Av, Sd)
Y = grand(m, n, "geom", p)
Y = grand(m, n, "poi", mu)
Y = grand(m, n, "def")
Y = grand(m, n, "unf", Low, High)
Y = grand(m, n, "uin", Low, High)
Y = grand(m, n, "lgi")

формируют матрицу размером m на n, элементы которой являются случайными числами. Все эти последовательности вызова могут быть расширены для создания гиперматрицы случайных чисел, у которой более двух размерностей, определённых в виде целых чисел, перечисленных перед типом статистического распределения:

Y = grand(m, n, o, ..., "..", ...)

Другой способ указать размеры ожидаемого вектора, матрицы или гиперматрицы случайных чисел:

Y = grand(X, ...)

где X - матрица или гиперматрица размером m на n на ... . В данном случае используются только размеры матрицы X.

Последовательности вызова:

Y = grand(n, "mn", Mean, Cov)
Y = grand(n, "markov", P, x0)
Y = grand(n, "mul", nb, P)
Y = grand(n, "prm", vect)

формируют матрицу размером m на n со случайными элементами, где m - размер аргумента Mean, Cov, P или vect в зависимости от ситуации (подробности ниже).

Последовательности вызова:

S = grand("getgen")
grand("setgen", gen)

S = grand("getsd")
grand("setsd", S)

grand("setcgn", G)
S = grand("getcgn")

grand("initgn", I)

grand("setall", s1, s2, s3, s4)

grand("advnst", K)

настраивают или запрашивают состояние имеющихся генераторов случайных чисел.

Получение случайных чисел по заданному закону распределения

бета-распределение

Y = grand(m, n, "bet", A, B) формирует случайные реализации по бета-распределению с параметрами A и B. Плотность бета-распределения лежит на интервале (0 < x < 1):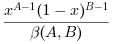

$\dfrac{x^{A-1}(1-x)^{B-1}}{\beta(A,B)}$

A и B должны быть вещественными числами >10^-37. С этой функцией связана функция cdfbet.

биномиальное распределение

Y = grand(m, n, "bin", N, p) формирует случайные реализации по биномиальному закону распределения с параметрами N (положительное целое) и p (вещественное число на интервале [0,1]): число "успехов" в серии из N независимых случайных (распределение Бернулли) экспериментов с вероятностью "успеха" в каждом из них p. С этой функцией связаны функции: binomial, cdfbin.

отрицательное биномиальное распределение

Y = grand(m, n, "nbn", N, p) формирует случайные реализации по отрицательному биномиальному распределению с параметрами N (положительное целое) и p (вещественное число на интервале (0,1)): число "неудач" случившихся до N-го "успеха" в последовательности испытаний с вероятностью "успеха" p. С этой функцией связана функция cdfnbn.

хи-квадрат распределение

Y = grand(m, n, "chi", Df) формирует случайные реализации по распределению хи-квадрат с Df степенями свободы. Число степеней свободы должно быть вещественным, строго больше нуля. С этой функцией связана функция: cdfchi.

нецентральное хи-квадрат распределение

Y = grand(m, n, "nch", Df, Xnonc) формирует случайные реализации по нецентральному хи-квадрат распределению с Df степенями свободы (вещественное значение >= 1.0) и параметром нецентральности Xnonc (вещественное число, больше либо равно нулю). С этой функцией связана функция: cdfchn.

экспоненциальное распределение

Y = grand(m, n, "exp", Av) формирует случайные реализации по экспоненциальному распределению с математическим ожиданием Av (вещественное значение, строго больше нуля).

F-распределение (отношение дисперсий, распределение Фишера)

Y = grand(m, n, "f", Dfn, Dfd) формирует случайные реализации по F-распределению (отношение дисперсий, распределение Фишера) с Dfn (вещественное значение, строго больше нуля) в числителе и Dfd степенями свободы (вещественное значение, строго больше нуля) в знаменателе. С этой функцией связана функция: cdff.

нецентральное F-распределение (отношение дисперсий)

Y = grand(m, n, "nf", Dfn, Dfd, Xnonc) формирует случайные реализации по нецентральному F-распределению (отношению дисперсий) с Dfn степенями свободы (вещественное значение, больше либо равно 1) в числителе, и Dfd степенями свободы (вещественное значение, строго больше нуля) в знаменателе и параметром нецентральности Xnonc (вещественное число, больше либо равно нулю). С этой функцией связана функция: cdffnc.

гамма-распределение

Y = grand(m, n, "gam", shape, rate) формирует случайные реализации по гамма-распределению с параметрами shape (вещественное значение, строго больше нуля) и rate (вещественное значение, строго больше нуля) (real > 0). Плотность гамма-распределения равна: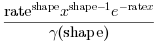

$\dfrac{ \textrm{rate}^{\textrm{shape}} x^{\textrm{shape}-1} e^{-\textrm{rate} x}}{\gamma(\textrm{shape}) }$

С этой функцией связаны: gamma, cdfgam.

распределение Гаусса-Лапласа (нормальное)

Y = grand(m, n, "nor", Av, Sd) формирует случайные реализации по нормальному распределению с математическим ожиданием Av (вещественное значение), среднеквадратичным отклонением Sd (вещественное значение, больше либо равно нулю). С этой функцией связана: cdfnor.

многомерное гауссовское (многомерное нормальное) распределение

Y = grand(n, "mn", Mean, Cov) формирует случайные реализации по многомерному гауссовскому распределению; среднее значение Mean должно быть вектор-столбцом размером m на 1, а ковариация Cov должна быть симметричной положительно определённой матрицей размером m на m (тогда Y будет матрицей размером m на n).

геометрическое распределение

Y = grand(m, n, "geom", p) формирует случайные реализации по геометрическому распределению с параметром p: количество независимых экспериментов (с вероятностью "успеха" p) до тех пор пока не будет "успех". Вероятность p должна быть в интервале [1.3e-307, 1]).

Y состоит из положительных целочисленных вещественных чисел, которые означают "число экспериментов, проведённых до первого успешного".

цепь Маркова

Y = grand(n, "markov", P, x0) формирует n последовательных состояний цепи Маркова, описанных матрицей переходных состояний P. Сумма элементов в каждой строке в P равна 1. Исходное состояние задаётся через x0. Если x0 является матрицей размером m=size(x0,"*"), то Y является матрицей размером m на n. Y(i,:) является выборочной траекторией, полученной из исходного состояния x0(i).

мультиномиальное (полиномиальное) распределение

Y = grand(n, "mul", nb, P) формирует n случайных реализаций по мультиномиальному распределению: совокупность nb событий в m категориях (положить nb "шаров" в m "ящиков"). P(i) является вероятностью того, что событие будет классифицировано в категории i. Вектор-столбец вероятностей P размером m-1 (вероятность категории m равна 1-sum(P)). Y имеет размер m на n. Каждый столбец Y(:,j) является случайной реализацией по мультиномиальному распределению, а Y(i,j) является количеством событий, попавших в категорию i (для j-того наблюдения) (sum(Y(:,j)) = nb).

распределение Пуассона

Y = grand(m, n, "poi", mu) формирует случайные реализации по распределению Пуассона с математическим ожиданием mu (вещественное значение, больше либо равно нулю). С этой функцией связана: cdfpoi.

случайные перестановки

Y = grand(n, "prm", vect) формирует n случайных перестановок vect. vect может быть вектор-столбцов вещественных чисел или вектором, матрицей или гиперматрицей комплексных, целых, логических, полиномиальных или строковых значений; полной или разрежённой. Из-за стековой структуры, vect не должен и не может быть вектор-строкой. Эта возможность перекрывает Matlab'овскую функцию randperm() поскольку randperm(n) эквивалентно grand(1,'prm',(1:n)'), а randperm(n, k) может быть получено через grand(1,'prm',(1:n)'); ans(1:k).

непрерывное равномерное распределение (def)

Y = grand(m, n, "def") формирует случайные реализации по равномерному распределению на интервале [0,1) (1 в интервал не входит).

непрерывное равномерное распределение (unf)

Y = grand(m, n, "unf", Low, High) формирует случайные вещественные значения равномерно распределённые на интервале [Low, High) (High в интервал не входит).

дискретное равномерное распределение (uin)

Y = grand(m, n, "uin", Low, High) формирует случайные целые числа, равномерно распределённые между значениями Low и High (включительно). High и Low должны быть такими целыми числами, что (High-Low+1) < 2.147483561e9.

равномерное распределение (lgi)

Y = grand(m, n, "lgi") возвращает базовый выход текущего генератора: случайные целые числа по равномерному распределению на интервалах:

[0, 2^32 - 1] для mt и kiss;
[0, 2^31 - 87] для clcg2;
[0, 2^31 - 2] для clcg4;
[0, 2^31 - 1] для urand.

Установка/получение текущего генератора и его состояния

У пользователя есть возможность выбирать между основными генераторами (которые дают случайные целые числа по распределению "lgi", другие получаются из него).

mt: Вихрь Марсенна (Mersenne-Twister), разработанный японскими учёными Макото Мацумото и Такудзи Нисимурой, период около 2^19937, состояние задаётся массивом из 624 целых чисел (плюс индекс на этот массив). Этот генератор используется по умолчанию.
kiss: "Keep It Simple Stupid" ("придерживайся простоты"), разработанный Джорджем Марсальи, период около 2^123, состояние задаётся четырьмя целыми числами.
clcg2: Комбинация двух линейных конгруэнтных генераторов П. Л'Экюйера (P. L'Ecuyer) с периодом около 2^61, состояние задаётся двумя целыми числами.
clcg4: Комбинация четырёх линейных конгруэнтных генераторов П. Л'Экюйера (P. L'Ecuyer) с периодом около 2^121, состояние задаётся четырьмя целыми числами. Этот генератор разделён на разные виртуальные (неперекрывающиеся) генераторы (101 генератор), которые могут быть полезными для разных задач (см. "Опции, специфичные для "clcg4"" и "Тестовый пример для "clcg4"").
urand: Генератор, используемый функцией Scilab'а rand, состояние задаётся одним целым числом, период 2^31. Этот генератор основан на "Urand, A Universal Random Number Generator" By, Michael A. Malcolm, Cleve B. Moler, Stan-Cs-73-334, January 1973, Computer Science Department, School Of Humanities And Sciences, Stanford University. Это самый быстрый генератор из данного списка, однако его статистические качества менее удовлетворительны по сравнению с другими генераторами.

Различные действия, общие для всех генераторов:

действие = "getgen"

S = grand("getgen") возвращает текущий основной генератор. В данном случае S является одной строкой из "mt", "kiss", "clcg2", "clcg4", "urand".

действие = "setgen"

grand("setgen",gen) устанавливает текущий основной генератор. В данном случае gen может быть одной строкой из "mt", "kiss", "clcg2", "clcg4", "urand". Заметьте, что этот вызов возвращает новый текущий генератор, т.е. gen.

действие = "getsd"

S = grand("getsd") получает текущее состояние (текущие семена) текущего основного генератора. S задаётся в виде вектор-столбца (целочисленных значений) с количеством элементов 625 для "mt" (первое значение является индексом в интервале [1,624]), 4 для "kiss", 2 для "clcg2", 4 для "clcg4" (для последнего вы получите текущее состояние текущего виртуального генератора) и 1 для "urand".

действие = "setsd"

grand("setsd", S) и grand("setsd", s1[, s2, s3, s4]) устанавливают состояние текущего основного генератора (несколько семян):

для mt

Sявляется вектор-столбцом целых чисел с количеством элементов 625 (значение первого элемента вектора является индексом и должно быть в интервале [1,624], а значения остальных 624 элементов должны лежать в интервале [0,2^32)), но не должны быть все нулями); более простая инициализация может быть сделана с помощью только одного целого числа s1 (s1 должно лежать в интервале [0,2^32));

для kiss

должны быть указаны четыре целых числа s1, s2, s3, s4 на интервале [0,2^32);

для clcg2

должны быть указаны два целых числа s1 на интервале [1,2^31-86] и s2 на интервале [1,2^31-250];

для clcg4

требуются четыре целых числа s1 на интервале [1,2^31-2], s2 на интервале [1,2^31-106], s3 на интервале [1,2^31-226], s4 на интервале [1,2^31-326];

Предостережение: с clcg4 вы устанавливаете семена текущего виртуального генератора, но вы можете потерять синхронизацию между ним и другими виртуальными генераторами (т.е. не гарантируется, что генерируемая последовательность не перекрывается с генерируемой последовательностью другого виртуального генератора) => вместо этого используйте опцию "setall".

для urand

должно быть указано одно целое число s1 на интервале [0,2^31).

действие = "phr2sd"

для заданной фразы phrase (символьной строки) Sd = grand("phr2sd", phrase) генерирует вектор Sd размером 1 на 2, который может использоваться в качестве семени для изменения состояния основного генератора (изначально подходил для clcg2).

Опции, специфичные для clcg4

Генератор clcg4 может использоваться как и остальные генераторы, но у него есть то преимущество, что он может быть разделён на несколько (101) виртуальных генераторов последовательности которых не перекрываются (когда вы используете классический генератор, то вы можете изменить исходное состояние (семена) для того, чтобы получить другую последовательность, но не гарантируется, что вы получите абсолютно другую последовательность). Каждому виртуальному генератору соответствует последовательность из 2^72 значений, которая далее делится на V=2^31 сегментов (или блоков) длиной W=2^41. Есть возможность вернуть заданный виртуальный генератор в начало последовательности или в начало текущего сегмента или перейти прямо к следующему сегменту. Можно также изменить исходное состояние (семя) генератора 0 с помощью опции "setall", которая затем изменит также исходное состояние остальных виртуальных генераторов так, чтобы получить синхронизацию, т.е. в функции нескольких исходных состояний генератора 0 исходные состояния генераторов 1...100 пересчитываются так, чтобы получить 101 неперекрывающуюся последовательность.

действие = "setcgn"

grand("setcgn",G) устанавливает текущий виртуальный генератор для clcg4 (когда clcg4 установлен, то есть используется виртуальный генератор (clcg4) номер G); виртуальные генераторы clcg4 пронумерованы 0, 1, ..., 100 (а поэтому G должно быть целым числом на интервале [0,100]); по умолчанию текущим виртуальным генератором является 0.

действие = "getcgn"

S = grand("getcgn") возвращает номер текущего виртуального генератора clcg4.

действие = "initgn"

grand("initgn", I) заново инициализирует состояние текущего виртуального генератора.

I = -1: устанавливает состояние в его исходное семя.
I = 0: устанавливает состояние в его последнее (предыдущее) семя (т. е. в начало текущего сегмента).
I = 1: устанавливает состояние на W значений нового семени от его последнего семени (т.е. в начало следующего сегмента) и сбрасывает параметры текущего сегмента.

действие = "setall"

grand("setall", s1, s2, s3, s4) устанавливает исходное состояние генератора 0 в s1, s2, s3, s4. Исходные семена других генераторов устанавливаются так, чтобы была синхронизация. Об ограничениях на s1, s2, s3, s4 смотри действие "setsd".

действие = "advnst"

grand("advnst", K) перемещает состояние текущего генератора вперёд на 2^K значений и сбрасывает исходное семя в это значение.

Примеры

В следующем примере мы генерируем случайные числа по различным законам распределения и строим соответствующие гистограммы.

// Возвращает матрицу размером 400 на 800 случайных чисел
// по нормальному распределению, с матожиданием 0 и дисперсией 1.
R = grand(400,800,"nor",0,1);
scf();
histplot(10,R);
xtitle("Случайные числа по нормальному закону распределения из функции grand","X","Частота");

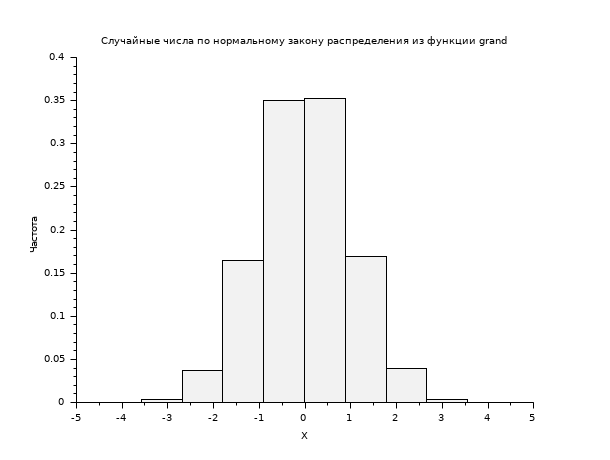
// Возвращает матрицу размером 400 на 800 случайных чисел
// с равномерным распределением в [0,1).
R = grand(400,800,"def");
scf();
histplot(10,R);
xtitle("Случайные числа с равномерным распределением из функции grand","X","Частота");

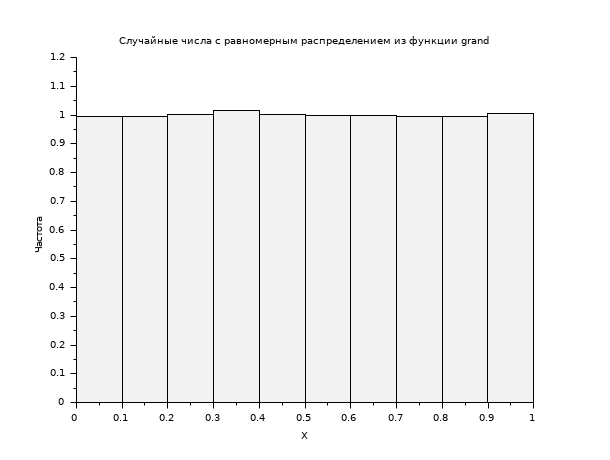
// Возвращает матрицу размером 400 на 800 случайных чисел
// по распределению Пуассона и матожиданием, равным 5.
R = grand(400,800,"poi",5);
scf();
histplot(10,R);
xtitle("Случайные числа по закону распределения Пуассона из grand","X","Частота");

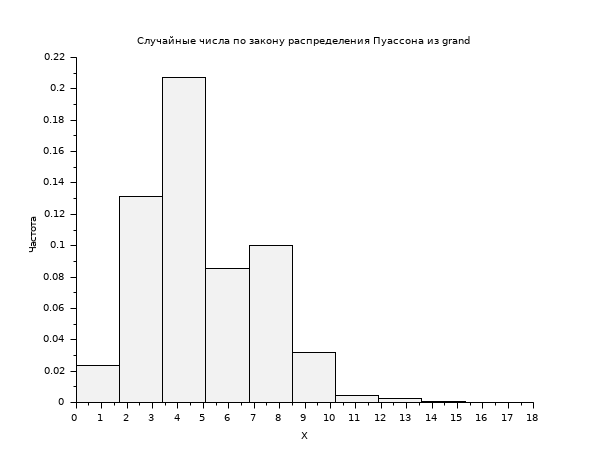
В следующем примере мы генерируем случайные числа по экспоненциальному распределению, а затем сравниваем эмпирическое распределение с теоретическим.

lambda=1.6;
N=100000;
X = grand(1,N,"exp",lambda);
scf();
classes = linspace(0,12,25);
histplot(classes,X);
x=linspace(0,12,25);
y = (1/lambda)*exp(-(1/lambda)*x);
plot(x,y,"ro-");
legend(["Эксперимент" "Теория"]);
xtitle("Случайные числа по экспоненциальному закону распределения из функции grand","X","Частота");

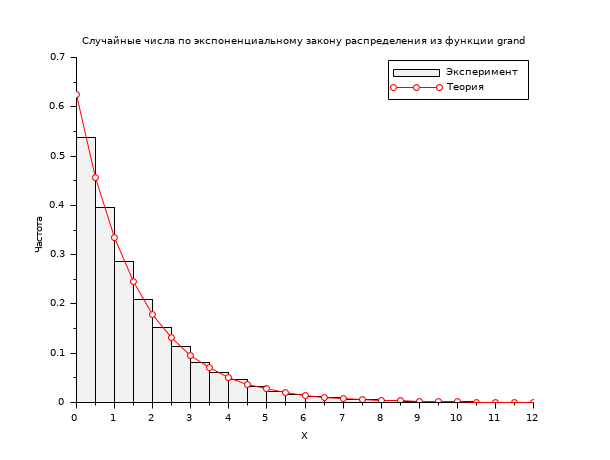
В следующем примере мы генерируем случайные числа по закону гамма- распределения, а затем сравниваем эмпирическое распределение с теоретическим.

N=10000;
A=10;
B=4;
R=grand(1,N,"gam",A,B);
XS=gsort(R,"g","i")';
PS=(1:N)'/N;
P=cdfgam("PQ",XS,A*ones(XS),B*ones(XS));
scf();
plot(XS,PS,"b-"); // Эмпирическое распределение
plot(XS,P,"r-"); // Теоретическое распределение
legend(["Эксперимент" "Теория"]);
xtitle("Интегральная функция распределения случайных чисел по закону гамма-распределения","X","F");

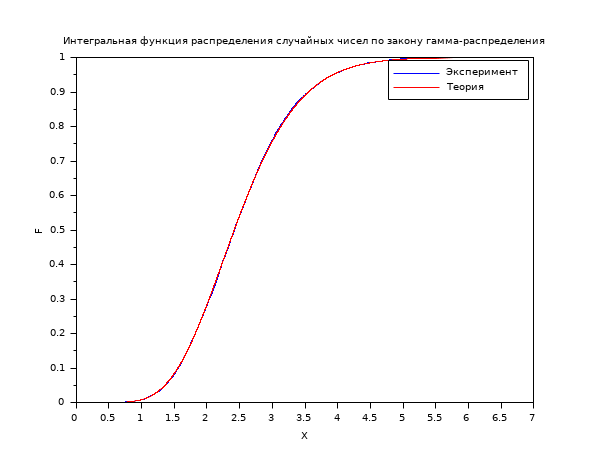
В следующем примере мы генерируем 10 случайных целых чисел в интервале [1,365].

grand(10,1,"uin",1,365)

В следующем примере мы генерируем 12 перестановок набора чисел [1, 2, ..., 7]. Эти 12 перестановок сохраняются столбец за столбцом.

grand(12,"prm",(1:7)')

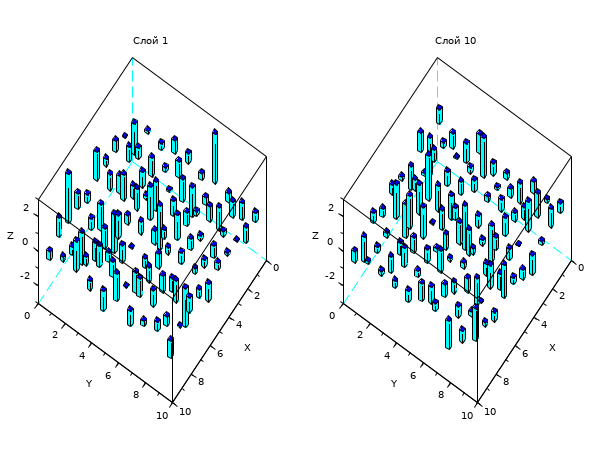
В следующем примере мы формируем гиперматрицу случайных чисел с "нормальным" распределением размерами 10 на 10 на 10 и строим гистограммы. Показываются первый и последний слои.

// Возвращает гиперматрицу случайных чисел с нормальным
// распределением, мат. ожидание 0 и среднеквадратичное отклонение 1, // размерами 10 на 10 на 10.
// Показаны только первый и последний слои.
R = grand(10,10,10,"nor",0,1);
subplot(1,2,1)
hist3d(R(:,:,1));
xtitle("Слой 1");
subplot(1,2,2)
hist3d(R(:,:,10));
xtitle("Слой 10");

Получение более или менее предсказуемых чисел

Генераторы псевдослучайных чисел основаны на детерминированных последовательностях. Для того, чтобы получить повторное воспроизведение моделирования, исходное семя генератора равно такой константе, что последовательность будет оставаться одной и той же от одной сессии к другой. Следовательно, по умолчанию, первые числа, производимые функцией grand, всегда одни и те же.

В некоторых ситуациях мы можем захотеть инициализировать семя генератора для того, чтобы получить менее предсказуемые числа. В этом случае мы можем инициализировать семя с помощью выходного значения функции getdate:

n=getdate("s");
grand("setsd",n)

Тестовый пример для clcg4

Пример необходимости возможности разделения clcg4 следующий. Сравниваются два статистических метода по данным разного размера. Первый является бутстреп-методом и считается точным при использовании меньшего количества данных, чем второй метод, который использует только грубую силу. Для первого метода будет генерироваться набор данных размером равномерно распределённым между 25 и 50. Затем будет генерироваться и анализироваться набор данных определённого размера. Второй метод будет выбирать размер набора данных между 100 и 200, генерировать данные и анализировать их. Этот процесс будет повторяться 1000 раз. Для уменьшения разброса мы хотим, чтобы числа, используемые в этих двух методах были одинаковыми для каждого из 1000 сравнений. Но второй метод будет использовать больше случайных чисел, чем первый метод и без этого пакета синхронизация была бы затруднительна. С clcg4 это легко. Используем генератор 0 для получения размера выборки для метода один и генератор 1 для получения данных. Затем сбрасываем состояние к начальному текущего блока и делаем то же самое для второго метода. Это гарантирует, что исходные данные для второго метода те же, что использовались в первом методе. Когда они оба закончатся, передвигаем вперёд блок для обоих генераторов.

Смотрите также

rand — Случайные числа
sprand — sparse random matrix
ssrand — генератор случайной системы

Report an issue
<< eye	Элементарные матрицы	linspace >>

Синтаксис

Аргументы

Описание

Получение случайных чисел по заданному закону распределения

Установка/получение текущего генератора и его состояния

Опции, специфичные для clcg4

Примеры

Получение более или менее предсказуемых чисел

Тестовый пример для clcg4

Смотрите также