Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
nyquist
nyquist plot
Syntax
nyquist( sl,[fmin,fmax] [,step] [,comments] [,symmetry]) nyquist( sl, frq [,comments] [,symmetry]) nyquist(frq,db,phi [,comments] [,symmetry]) nyquist(frq, repf [,comments] [,symmetry])
Arguments
- sl
A siso or simo linear dynamical system, in state space, transfer function or zpk representations, in continuous or discrete time.
- fmin,fmax
real scalars (frequency lower and upper bounds (in Hz)).
- step
real (logarithmic discretization step), if not given an adaptative discretization is used.
- comments
string vector (captions).
- symmetry
a boolean, default value is %t.
- frq
vector or matrix of frequencies (in Hz) (one row for each output of
sl).- db,phi
real matrices of modulus (in dB) and phases (in degree) (one row for each output of
sl).- repf
matrix of complex numbers. Frequency response (one row for each output of
sl)
Description
Nyquist plot i.e Imaginary part versus Real part of the
frequency response of sl. If the
symmetry argument is true or omitted the
Nyquist plot displays the symmetric graph (positive and negative
frequencies).
For continuous time systems sl(2*%i*%pi*w) is
plotted. For discrete time system or discretized systems
sl(exp(2*%i*%pi*w*fd) is used ( fd=1
for discrete time systems and fd=sl('dt') for
discretized systems )
sl can be a continuous-time or
discrete-time SIMO system given by its state space,
rational transfer function (see syslin) or zpk representation. In case of
multi-output the outputs are plotted with different
colors.
The frequencies are given by the bounds fmin,fmax
(in Hz) or by a row-vector (or a matrix for multi-output)
frq.
step is the ( logarithmic ) discretization step.
(see calfrq for the choice of default value).
comments is a vector of character strings
(captions).
db,phi are the matrices of modulus (in Db) and
phases (in degrees). (One row for each response).
repf is a matrix of complex numbers. One row for
each response.
Default values for fmin and
fmax are 1.d-3,
1.d+3 if sl is continuous-time or
1.d-3, 0.5/sl.dt (nyquist frequency)
if sl is discrete-time.
Automatic discretization of frequencies is made by calfrq.
To obtain the value of the frequency at a selected point(s) you can activate the datatips manager and click the desired point on the nyquist curve(s).
Graphics entities organization
The nyquist function creates a compound
object for each SISO system. The following piece of code allows
to get the handle on the compound object of the ith system:
ax=gca();//handle on current axes hi=ax.children($+i-1)// the handle on the compound object of the ith system
This compound object has two children: a compound object that defines the small arrows (a compound of small polylines) and the curve labels (a compound of texts) and a polyline which is the curve itself. The following piece of code shows how one can customize a particular nyquist curve display.
hi.children(1).visible='off'; //hides the arrows and labels hi.children(2).thickness=2; //make the curve thicker
Examples
//Nyquist curve s=poly(0,'s') h=syslin('c',(s^2+2*0.9*10*s+100)/(s^2+2*0.3*10.1*s+102.01)); h1=h*syslin('c',(s^2+2*0.1*15.1*s+228.01)/(s^2+2*0.9*15*s+225)) clf(); nyquist(h1) // add a datatip ax=gca(); h_h=ax.children($).children(2);//handle on Nyquist curve of h tip=datatipCreate(h_h,[1.331,0.684]); datatipSetOrientation(tip,"upper left");
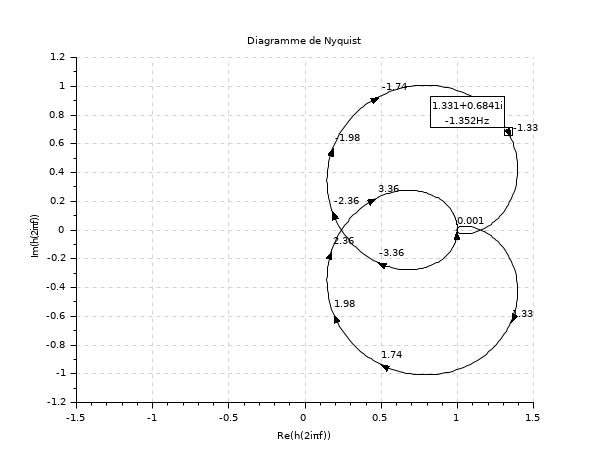
//Hall chart as a grid for nyquist s=poly(0,'s'); Plant=syslin('c',16000/((s+1)*(s+10)*(s+100))); //two degree of freedom PID tau=0.2;xsi=1.2; PID=syslin('c',(1/(2*xsi*tau*s))*(1+2*xsi*tau*s+tau^2*s^2)); clf(); nyquist([Plant;Plant*PID],0.5,100,["Plant";"Plant and PID corrector"]); hallchart(colors=color('light gray')*[1 1]) //move the caption in the lower right corner ax=gca();Leg=ax.children(1); Leg.legend_location="in_upper_left";

See also
- syslin — définition d'un système dynamique linéaire
- bode — Bode plot
- black — Black-Nichols diagram of a linear dynamical system
- nyquistfrequencybounds — Computes the frequencies for which the nyquist locus enters and leaves a given rectangle.
- calfrq — frequency response discretization
- freq — frequency response
- repfreq — frequency response
- phasemag — phase and magnitude computation
- datatips — Tool for placing and editing tips along the plotted curves
History
| Version | Description |
| 6.0 | handling zpk representation |
| Report an issue | ||
| << nicholschart | Domaine de fréquence | nyquistfrequencybounds >> |