Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
number_properties
determine floating-point parameters
Syntax
pr = number_properties(prop)
Arguments
- prop
string
- pr
real or boolean scalar
Description
This function may be used to get the characteristic
numbers/properties of the floating point set denoted here by
F(b,p,emin,emax) (usually the 64 bits float numbers set
prescribe by IEEE 754). Numbers of F are of the
form:
sign * m * b^e
e is the exponent and m the
mantissa:
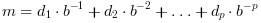
 the digits are in
the digits are in [0, b-1]
and e in [emin, emax], the number is
said "normalized" if 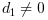 . The following queries may be used:
. The following queries may be used:
- prop = "radix"
then
pris the radixbof the setF- prop = "digits"
then
pris the number of digitsp- prop = "huge"
then
pris the max positive float ofF- prop = "tiny"
then
pris the min positive normalized float ofF- prop = "denorm"
then
pris a boolean (%t if denormalized numbers are used)- prop = "tiniest"
then if denorm = %t,
pris the min positive denormalized number elsepr= tiny- prop = "eps"
then
pris the epsilon machine ( generally ( ) which is the relative max error
between a real
) which is the relative max error
between a real x(such than|x|in[tiny, huge]) andfl(x), its floating point approximation inF- prop = "minexp"
then
prisemin- prop = "maxexp"
then
prisemax
 | This function uses the lapack routine dlamch to get the machine
parameters (the names (radix, digit, huge, etc...) are those recommended by the LIA 1
standard and are different from the corresponding lapack's ones). |
 | Sometimes you can see the following definition for the epsilon machine :
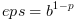 but in this function we use the traditional one
(see prop = "eps" before) and so
but in this function we use the traditional one
(see prop = "eps" before) and so 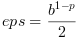 if normal rounding occurs, and
if normal rounding occurs, and 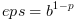 otherwise.
otherwise. |
Examples
b = number_properties("radix") eps = number_properties("eps")
See also
| Report an issue | ||
| << nextpow2 | Virgule flottante | round >> |