Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
number_properties
определение параметров чисел с плавающей запятой
Синтаксис
pr = number_properties(prop)
Аргументы
- prop
строка
- pr
вещественный или логический скаляр
Описание
Эта функция может быть использована для получения характеристик
чисел/свойств из набора с плавающей запятой, обозначенного здесь как
F(b,p,emin,emax) (обычно набор 64-х разрядных чисел
описывается IEEE 754). Числа F представляются в
виде:
sign * m * b^e
e - показатель, а
m - мантисса:
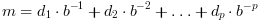
Разряды 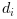 находятся в диапазоне
находятся в диапазоне [0,
b-1]
а e находится в диапазоне
[emin, emax], скажем, что число "нормированное", если
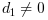 . Можно получить следующие сведения:
. Можно получить следующие сведения:
- prop = "radix"
тогда
prявляется основание логарифмаbнабораF- prop = "digits"
тогда
prявляется количеством разрядовp- prop = "huge"
тогда
prявляется максимальным положительным числом с плавающей запятой изF- prop = "tiny"
тогда
prявляется минимальным положительным нормированным числом с плавающей запятой изF- prop = "denorm"
тогда
prявляется логическим значением (%t, если используются ненормированные числа)- prop = "tiniest"
тогда, если
denorm = %t, тоprявляется минимальным положительным ненормированным числом, в противном случаеpr = tiny- prop = "eps"
тогда
prявляется машинным эпсилоном (вообще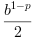 ), которое является относительной
максимальной ошибкой между вещественным
), которое является относительной
максимальной ошибкой между вещественным x(таким, что|x|в[tiny, huge]) иfl(x), его приближением с плавающей запятой вF- prop = "minexp"
тогда
prявляетсяemin- prop = "maxexp"
тогда
prявляетсяemax
 | Эта функция использует подпрограмму dlamch для получения параметров
машины (имена (radix, digit, huge и т. д.) рекомендованы стандартом LIA 1
и отличаются от соответствующих имён lapack). |
 | иногда вы можете увидеть следующее определение машинного эпсилона:
 ,но в этой функции мы используем традиционное определение
(см. выше prop = "eps") и поэтому ,но в этой функции мы используем традиционное определение
(см. выше prop = "eps") и поэтому 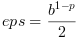 , если производится нормальное округление, а
если нет, то
, если производится нормальное округление, а
если нет, то 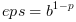 . . |
Примеры
b = number_properties("radix") eps = number_properties("eps")
Смотрите также
| Report an issue | ||
| << nextpow2 | Плавающая запятая | round >> |