Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
frep2tf
transfer function realization from frequency response
Syntax
[h [,err]]=frep2tf(frq,repf,dg [,dom,tols,weight])
Arguments
- frq
vector of frequencies in Hz.
- repf
vector of frequency response
- dg
degree of linear system
- dom
time domain (
'c'or'd'ordt)- tols
a vector of size 3 giving the relative and absolute tolerance and the maximum number of iterations (default values are
rtol=1.e-2; atol=1.e-4, N=10).- weight
vector of weights on frequencies
- h
SISO transfer function
- err
error (for example if
dom='c'sum(abs(h(2i*pi*frq) - rep)^2)/size(frq,*))
Description
Frequency response to transfer function conversion. The order of h
is a priori given in dg which must be provided.
The following linear system is solved in the least square sense.
weight(k)*(n( phi_k) - d(phi_k)*rep_k)=0, k=1,..,n
where phi_k= 2*%i*%pi*frq when dom='c' and
phi_k=exp(2*%i*%pi*dom*frq if not. If the weight
vector is not given a default
penalization is used (when dom='c').
A stable and minimum phase system can be obtained by using function factors.
Examples
s=poly(0,'s'); h=syslin('c',(s-1)/(s^3+5*s+20)) frq=0:0.05:3; repf=repfreq(h,frq); clean(frep2tf(frq,repf,3))
Sys=ssrand(1,1,10); frq=logspace(-3,2,200); [frq,rep]=repfreq(Sys,frq); //Frequency response of Sys [Sys2,err]=frep2tf(frq,rep,10); Sys2=clean(Sys2) //Sys2 obtained from freq. resp of Sys [frq,rep2]=repfreq(Sys2,frq); //Frequency response of Sys2 clf(); bode(frq,[rep;rep2]) //Responses of Sys and Sys2 [gsort(spec(Sys('A'))), gsort(roots(Sys2('den')))] //poles
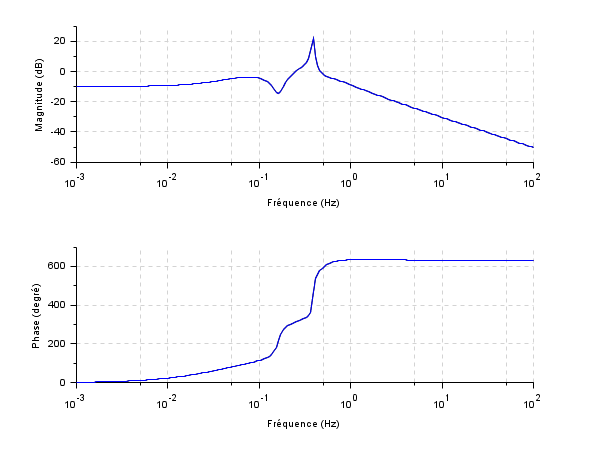
dom = 1/1000; // Sampling time z = poly(0,'z'); h = syslin(dom,(z^2+0.5)/(z^3+0.1*z^2-0.5*z+0.08)) frq = (0:0.01:0.5)/dom; repf = repfreq(h,frq); [Sys2,err] = frep2tf(frq,repf,3,dom); [frq,rep2] = repfreq(Sys2,frq); //Frequency response of Sys2 clf(); plot2d(frq, abs([repf;rep2])')

See also
| Report an issue | ||
| << des2tf | Linear System Representation | lsslist >> |