Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
nyquistfrequencybounds
Computes the frequencies for which the nyquist locus enters and leaves a given rectangle.
Syntax
[fmin,fmax] = nyquistfrequencybounds(H,bounds)
Parameters
- H
A SISO linear dynamical system.
- bounds
A 2 by 2 array: [Rmin Imin;Rmax Imax] that defines a complex-plane rectangle.
- fmin
a real: the lowest frequency (Hz) such that the nyquist locus enters the given rectangle or 0 if the 0 Hz point lies in the rectangle or [] if the locus is completely outside the rectangle.
- fmax
a real: the highest frequency (Hz) such that the nyquist locus leaves the given rectangle or %inf if the %inf (hz) point is in the rectangle or [] if the locus is completely outside the rectangle.
Description
Given a C plane rectangle,
nyquistfrequencybounds Computes the lowest
frequency for which the nyquist locus enters the rectangle and
the highest frequency for which the nyquist locus leaves the
rectangle.
Examples
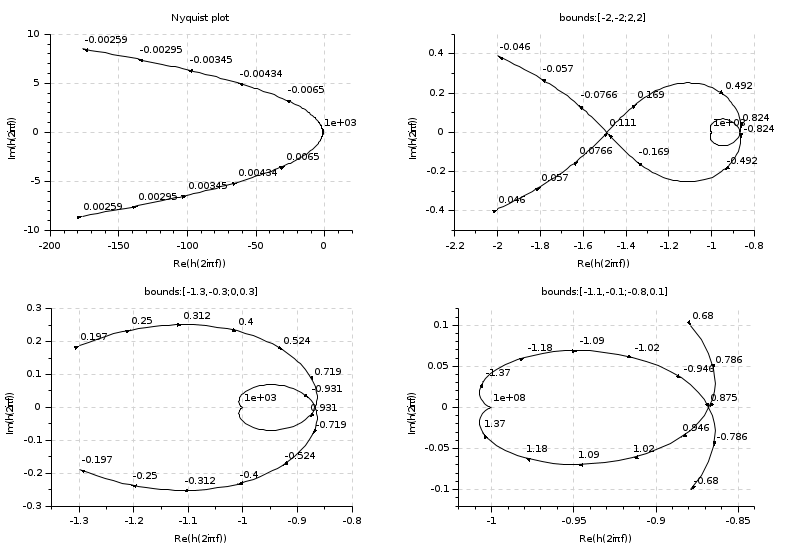
s=%s num=2+9*s-9*s^2-11*s^3+0.01*s^4; den=43*s^2+65*s^3+34*s^4+8*s^5+s^6+0.1*s^7 H=syslin('c',num,den)-1 clf;set(gcf(),'axes_size',[805,549]) subplot(221) nyquist(H) subplot(222) bounds=[-2 -2;2 2] [fmin,fmax]=nyquistfrequencybounds(H,bounds) nyquist(H,fmin,fmax) title("bounds:"+sci2exp(bounds,0)); subplot(223) bounds=[-1.3 -0.3;0 0.3] [fmin,fmax]=nyquistfrequencybounds(H,bounds) nyquist(H,fmin,fmax) title("bounds:"+sci2exp(bounds,0)); subplot(224) bounds=[-1.1 -0.1;-0.8 0.1] [fmin,fmax]=nyquistfrequencybounds(H,bounds) nyquist(H,fmin,1d8) title("bounds:"+sci2exp(bounds,0));
See also
| Report an issue | ||
| << nyquist | Frequency Domain | phasemag >> |