histplot

Arguments

n

positive integer (number of classes)

x

increasing vector defining the classes (x may have at least 2 components)

data

vector (data to be analysed)

normalization

a boolean (%t (default value) or %f)

polygon

a boolean (%t or %f (default value))

<opt_args>

This represents a sequence of statements key1=value1,key2=value2 ,... where key1, key2,... can be any optional plot2d parameter (style,strf,leg, rect,nax, logflag,frameflag, axesflag ).

cf

This represents a sequence of statements key1=value1,key2=value2 ,... where key1, key2,... can be any optional plot2d parameter (style,strf,leg, rect,nax, logflag,frameflag, axesflag ).

ind

This represents a sequence of statements key1=value1,key2=value2 ,... where key1, key2,... can be any optional plot2d parameter (style,strf,leg, rect,nax, logflag,frameflag, axesflag ).

Description

This function plots a histogram of the data vector using the classes x. When the number n of classes is provided instead of x, the classes are chosen equally spaced and x(1) = min(data) < x(2) = x(1) + dx < ... < x(n+1) = max(data) with dx = (x(n+1)-x(1))/n.

The classes are defined by C1 = [x(1), x(2)] and Ci = ( x(i), x(i+1)] for i >= 2. Noting Nmax the total number of data (Nmax = length(data)) and Ni the number of data components falling in Ci, the value of the histogram for x in Ci is equal to Ni/(Nmax (x(i+1)-x(i))) when normalization is true (default case) and else, simply equal to Ni. When normalization occurs the histogram verifies:

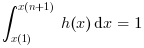
when x(1)<=min(data) and max(data) <= x(n+1)

Any plot2d (optional) parameter may be provided; for instance to plot a histogram with the color number 2 (blue if std colormap is used) and to restrict the plot inside the rectangle [-3,3]x[0,0.5], you may use histplot(n,data, style=2, rect=[-3,0,3,0.5]).

Frequency polygon is a line graph drawn by joining all the midpoints of the top of the bins of a histogram. Therefore we can use histplot function to plot a polygon frequency chart.

The optional argument polygon connects the midpoint of the top of each bar of a histogram with straight lines.

If polygon=%t we will have a histogram with frequency polygon chart.

Enter the command histplot() to see a demo.

Examples

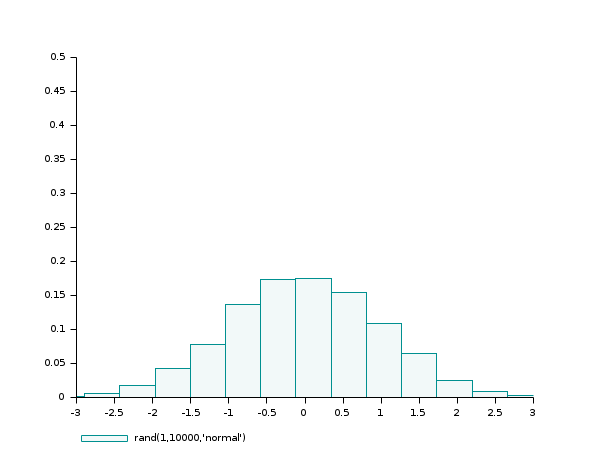
• Example #1: variations around a histogram of a gaussian random sample

  d=rand(1,10000,'normal');  // the gaussian random sample
  clf(); histplot(20,d)
  clf(); histplot(20,d,normalization=%f)
  clf(); histplot(20,d,leg='rand(1,10000,''normal'')',style=5)
  clf(); histplot(20,d,leg='rand(1,10000,''normal'')',style=16, rect=[-3,0,3,0.5]);

  
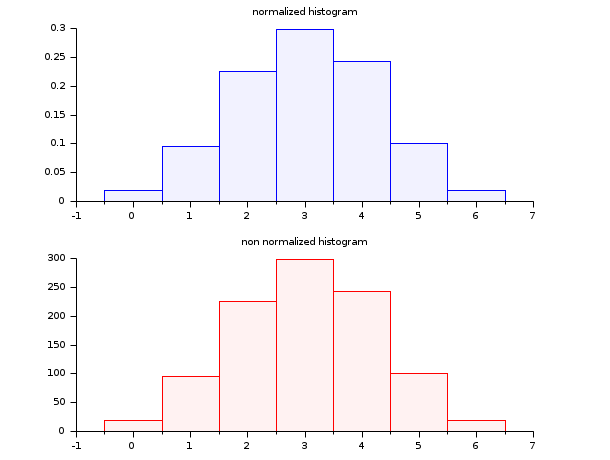
• Example #2: histogram of a binomial (B(6,0.5)) random sample

  d = grand(1000,1,"bin", 6, 0.5);
  c = linspace(-0.5,6.5,8);
  clf()
  subplot(2,1,1)
  histplot(c, d, style=2)
  xtitle("Normalized histogram")
  subplot(2,1,2)
  histplot(c, d, normalization=%f, style=5)
  xtitle("Non normalized histogram")

  
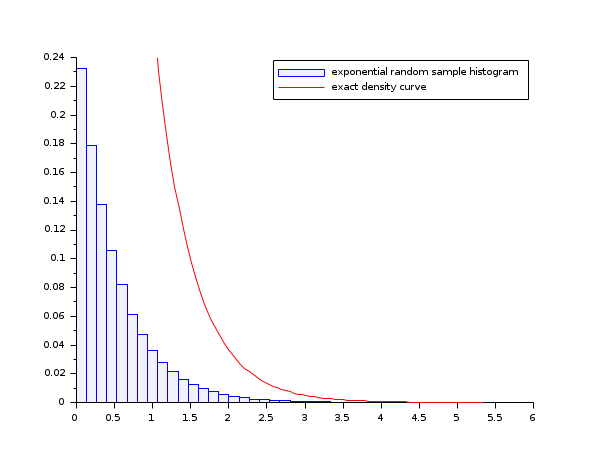
• Example #3: histogram of an exponential random sample

  lambda = 2;
  X = grand(100000,1,"exp", 1/lambda);
  Xmax = max(X);
  clf()
  histplot(40, X, style=2)
  x = linspace(0,max(Xmax),100)';
  plot2d(x,lambda*exp(-lambda*x),strf="000",style=5)
  legend(["exponential random sample histogram" "exact density curve"]);

  
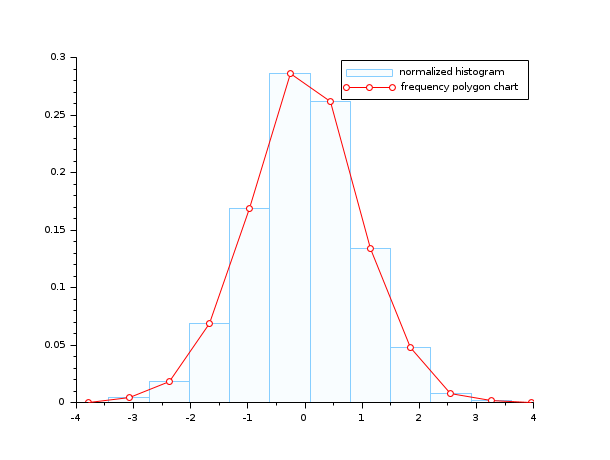
• Example #4: the frequency polygon chart and the histogram of a gaussian random sample

  n=10;
  data=rand(1,1000,"normal");
  clf(); histplot(n, data, style=12, polygon=%t);
  legend(["normalized histogram" "frequency polygon chart"]);

  

See also

• histc — computes an histogram
• hist3d — 3D representation of a histogram
• plot2d — 2D plot
• bar — bar histogram
• dsearch — поиск в упорядоченных наборах