Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
householder
Householder orthogonal reflexion matrix. Symetrical wrt a plane
Syntax
householder() // demo u = householder(v [,w]) [u, H] = householder(v [,w])
Arguments
- v
real or complex column vector
- w
real or complex column vector with same size as
v. Default value iseye(v)((Ox) axis).- u
unit vector lying in the
(v,w)plane and orthogonal to the bisectrix of(v,w). Column of size(v) of real or complex numbers.- H
Orthogonal Householder reflexion matrix:
H= eye() - 2*u*u'.His such thatinv(H)==H,H'==H, anddet(H)==-1.If
vandware real,H*vis proportional tow.
Description
householder(..) computes the unit vector u
lying in the (v,w) plane and orthogonal to the bisectrix of
(v,w).
If v and w are proportional:
If they are opposite,
u= v/|v|is returned.- If they are real and have the same direction,
uis set in the (xOy) plane with a prioriu(1)>0, and orthogonal tov(u'*v==0). However,- If they are along (Ox),
u = (Oy+)is returned instead. - If
vandware scalars with same signs, the orthogonal sub-space is restricted to{0}that can't be normalized:uandHare then set to%nan.
- If they are along (Ox),
 | If the related reflexion matrix H is computed, for any point A
of column coordinates a, H*a are the coordinates of
the symetrical image of A with respect to the (v,w) plane
(see the example below). |
 | If v or/and w are in row, they are priorly
transposed into columns. |
 | If v or/and w are [],
[] is returned for u and H. |
Examples
a = [ rand(1,1) 0 0 ]'; [ra hm] = householder(a); [a ra hm*a ] norm(ra) b = rand(3,1); [rb, hm] = householder(b); [b rb eye(b) clean(hm*b) ] norm(rb) [rb2b, hm] = householder(b, 2*b); [b rb2b clean(hm*b ./ b) ] // last column must be uniform norm(rb2b) // must be 1 c = rand(3,1); [rbc, hm] = householder(b,c); norm(rbc) // must be 1 hm*b ./c // must be uniform d = b + %i*c; e = rand(3,1) + %i*rand(3,1); [rde, hm] = householder(d,e); norm(rbc) // must be 1 clean(inv(hm) - hm) // must be zeros(3,3) clean(hm' - hm) // must be zeros(3,3) clean(det(hm)) // must be -1
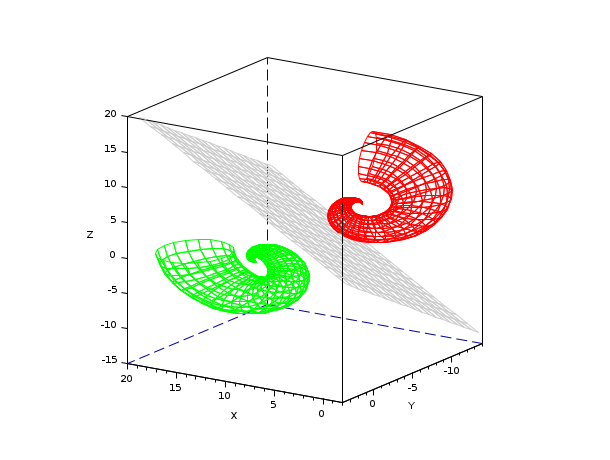
Application: Symetrical image of an object w.r.t. a given plane
// (OA) = [0 0 1] is reflected in O into (OB) = [ 1 1 0.3 ]: [n, H] = householder([0 0 1]', [ 1 1 0.3 ]'); // "n" is the unit vector orthogonal to the reflecting plane // Emitting object (feature from shell demo): u = linspace(0,2*%pi,40); v = linspace(0,2*%pi,20); Xe = (cos(u).*u)'*(1+cos(v)/2)+10; Ye = (u/2)'*sin(v); Ze = (sin(u).*u)'*(1+cos(v)/2); // Symetrical object: Pe = [ Xe(:)' ; Ye(:)' ; Ze(:)']; Pr = H*Pe; Xr = matrix(Pr(1,:),40,-1); Yr = matrix(Pr(2,:),40,-1); Zr = matrix(Pr(3,:),40,-1); // Reflecting plane containing O: n(1).x + n(2).y + n(3).z = 0 // Sampling space: x = linspace(min([Xe(:);Xr(:)]), max([Xe(:);Xr(:)]),20); y = linspace(min([Ye(:);Yr(:)]), max([Ye(:);Yr(:)]),20); [X, Y] = meshgrid(x,y); // Generating the mirror: deff("z = mirror(x,y,n)","z = -n(1)/n(3)*x - n(2)/n(3)*y") Zm = mirror(X,Y,n); // Plotting: clf() isoview() drawlater() f = gcf(); f.color_map = [ 0.8 0.8 0.8 ; jetcolormap(100)]; surf(Xe,Ye,Ze) surf(X,Y,Zm) surf(Xr,Yr,Zr) a = gca(); a.rotation_angles = [74 123]; a.children.color_flag = 0; a.children.color_mode = 0; a.children(1).foreground = color("red"); a.children(2).foreground = 1; a.children(3).foreground = color("green"); drawnow()
History
| バージョン | 記述 |
| 6.0 | Householder reflexion matrix added as second output parameter. Demo householder() added. Help page reviewed. |
| Report an issue | ||
| << givens | Factorization | sqroot >> |