Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
histc
ヒストグラムを計算
呼び出し手順
[cf, ind] = histc(n, data [,normalization]) [cf, ind] = histc(x, data [,normalization])
引数
- n
正の整数 (クラスの数)
- x
クラスを定義する漸増ベクトル (
xには最低2つの要素があります)- data
ベクトル (解析対象のデータ)
- cf
nまたはxにより定義されるクラスに含まれるdataの値の数を示すベクトル- ind
dataと同じ大きさのベクトルまたは行列で, データdataの各要素がnまたはxにより定義された クラスに重複して属していることを示します- normalization
スカラー論理値.
normalization=%f (デフォルト):cfは,各クラスにおける点の総数を表します.normalization=%t:cfは,各クラスにおける点の数を点の総数に関して相対的に表します.
説明
この関数は,クラスxによりdataベクトルの
ヒストグラムを計算します.
xではなくクラスの数 nが指定された場合,等間隔で
x(1) = min(data) < x(2) = x(1) + dx < ... < x(n+1) = max(data)
(ただし, dx = (x(n+1)-x(1))/n)となるクラスが選択されます.
クラスはC1 = [x(1), x(2)] および Ci = ( x(i), x(i+1)]
(i >= 2)で定義されます.
Nmaxはdataの総数 (Nmax = length(data)),
NiはCiに含まれるdata要素の数,
Ciにおけるxのヒストグラムの値は,
"normalized"が選択された場合は
Ni/(Nmax (x(i+1)-x(i))) となり,
そうでない場合は単にNiとなります.
正規化が行われた際,ヒストグラムは以下を確認します:
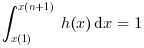
x(1)<=min(data) および max(data) <= x(n+1) の場合
例
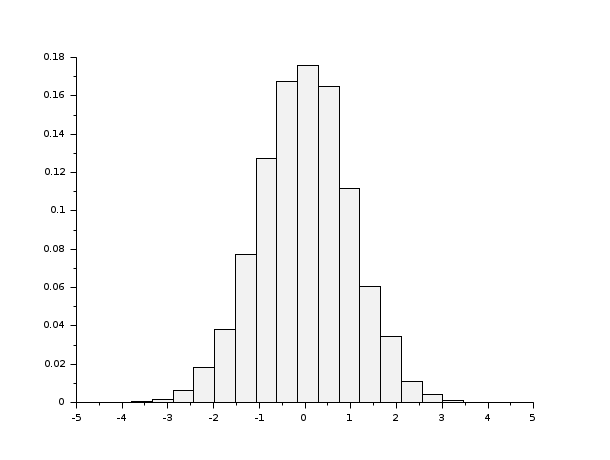
- 例 #1: ガウス乱数標本のヒストグラム周辺の変化
// ガウス乱数標本 d = rand(1, 10000, 'normal'); [cf, ind] = histc(20, d, normalization=%f) // グラフィック表現を示すためにhistplotを使用 clf(); histplot(20, d, normalization=%f); [cf, ind] = histc(20, d) clf(); histplot(20, d);
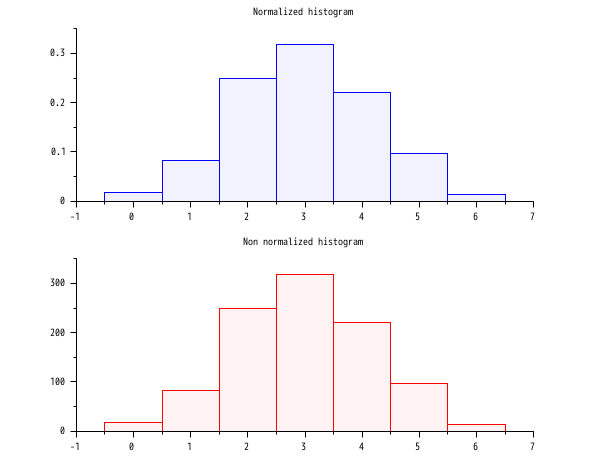
- 例 #2: 二項(B(6,0.5)) 乱数標本のヒストグラム
d = grand(1000,1,"bin", 6, 0.5); c = linspace(-0.5,6.5,8); clf() subplot(2,1,1) [cf, ind] = histc(c, d) histplot(c, d, style=2); xtitle(_("Normalized histogram")) subplot(2,1,2) [cf, ind] = histc(c, d, normalization=%f) histplot(c, d, normalization=%f, style=5); xtitle(_("Non normalized histogram"))
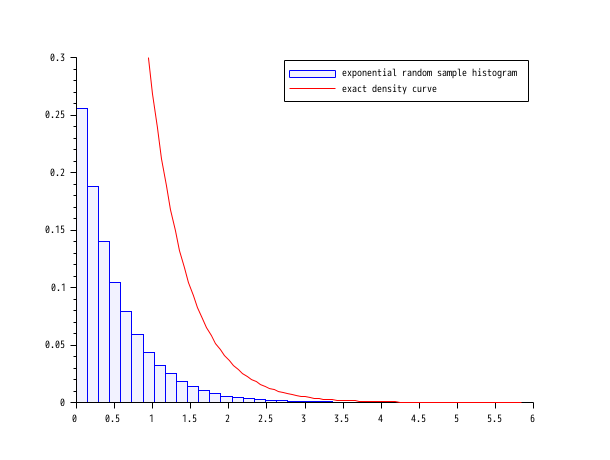
- 例 #3: 指数乱数標本のヒストグラム
lambda = 2; X = grand(100000,1,"exp", 1/lambda); Xmax = max(X); [cf, ind] = histc(40, X) clf() histplot(40, X, style=2); x = linspace(0, max(Xmax), 100)'; plot2d(x, lambda*exp(-lambda*x), strf="000", style=5) legend([_("exponential random sample histogram") _("exact density curve")]);
- 例 #4: ガウス乱数標本の周波数ポリゴンチャートとヒストグラム
n = 10; data = rand(1, 1000, "normal"); [cf, ind] = histc(n, data) clf(); histplot(n, data, style=12, polygon=%t); legend([_("normalized histogram") _("frequency polygon chart")]);
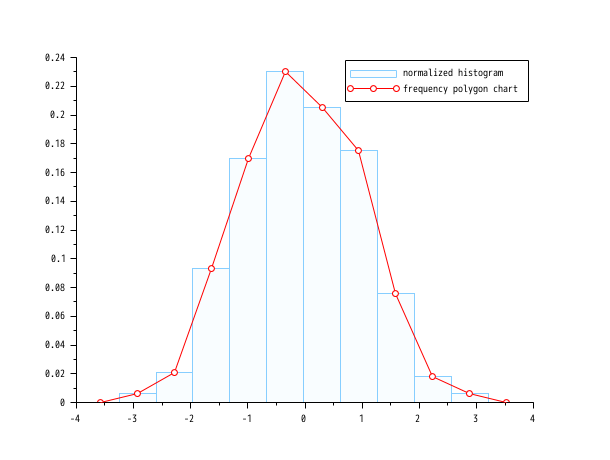
参照
履歴
| バージョン | 記述 |
| 5.5.0 | Introduction |
| Report an issue | ||
| << covar | Descriptive Statistics | median >> |